
Variable-length code
Encyclopedia
In coding theory
a variable-length code is a code
which maps source symbols to a variable number of bits.
Variable-length codes can allow sources to be compressed
and decompressed with zero error (lossless data compression
) and still be read back symbol by symbol. With the right coding strategy an independent and identically-distributed source may be compressed almost arbitrarily close to its entropy
. This is in contrast to fixed length coding methods, for which data compression is only possible for large blocks of data, and any compression beyond the logarithm of the total number of possibilities comes with a finite (though perhaps arbitrarily small) probability of failure.
Some examples of well-known variable-length coding strategies are Huffman coding
, Lempel–Ziv coding and arithmetic coding
.
Using terms from formal language theory, the precise mathematical definition is as follows: Let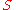 and
and  be two finite sets, called the source and target alphabets, respectively. A code
be two finite sets, called the source and target alphabets, respectively. A code 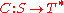 is a total function mapping each symbol from
is a total function mapping each symbol from 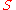 to a sequence of symbols over
to a sequence of symbols over  , and the extension of
, and the extension of  to a homomorphism of
to a homomorphism of  into
into  , which naturally maps each sequence of source symbols to a sequence of target symbols, is referred to as its extension.
, which naturally maps each sequence of source symbols to a sequence of target symbols, is referred to as its extension.
.
A special case of prefix codes are block code
s. Here all codewords must have the same length. The latter are not very useful in the context of source coding
, but often serve as error correcting codes
in the context of channel coding.
codeword length. For the above example, if the probabilities of (a, b, c, d) were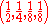 , the expected number of bits used to represent a source symbol using the code above would be:
, the expected number of bits used to represent a source symbol using the code above would be:
As the entropy of this source is 1.7500 bits per symbol, this code compresses the source as much as possible so that the source can be recovered with zero error.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
a variable-length code is a code
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
which maps source symbols to a variable number of bits.
Variable-length codes can allow sources to be compressed
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
and decompressed with zero error (lossless data compression
Lossless data compression
Lossless data compression is a class of data compression algorithms that allows the exact original data to be reconstructed from the compressed data. The term lossless is in contrast to lossy data compression, which only allows an approximation of the original data to be reconstructed, in exchange...
) and still be read back symbol by symbol. With the right coding strategy an independent and identically-distributed source may be compressed almost arbitrarily close to its entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
. This is in contrast to fixed length coding methods, for which data compression is only possible for large blocks of data, and any compression beyond the logarithm of the total number of possibilities comes with a finite (though perhaps arbitrarily small) probability of failure.
Some examples of well-known variable-length coding strategies are Huffman coding
Huffman coding
In computer science and information theory, Huffman coding is an entropy encoding algorithm used for lossless data compression. The term refers to the use of a variable-length code table for encoding a source symbol where the variable-length code table has been derived in a particular way based on...
, Lempel–Ziv coding and arithmetic coding
Arithmetic coding
Arithmetic coding is a form of variable-length entropy encoding used in lossless data compression. Normally, a string of characters such as the words "hello there" is represented using a fixed number of bits per character, as in the ASCII code...
.
Codes and their extensions
The extension of a code is the mapping of finite length source sequences to finite length bit strings, that is obtained by concatenating for each symbol of the source sequence the corresponding codeword produced by the original code.Using terms from formal language theory, the precise mathematical definition is as follows: Let
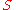 and
and  be two finite sets, called the source and target alphabets, respectively. A code
be two finite sets, called the source and target alphabets, respectively. A code 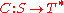 is a total function mapping each symbol from
is a total function mapping each symbol from 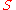 to a sequence of symbols over
to a sequence of symbols over  , and the extension of
, and the extension of  to a homomorphism of
to a homomorphism of  into
into  , which naturally maps each sequence of source symbols to a sequence of target symbols, is referred to as its extension.
, which naturally maps each sequence of source symbols to a sequence of target symbols, is referred to as its extension.Classes of variable-length codes
Variable-length codes can be strictly nested in order of decreasing generality as non-singular codes, uniquely decodable codes and prefix codes. Prefix codes are always uniquely decodable, and these in turn are always non-singular:Non-singular codes
A code is non-singular if each source symbol is mapped to a different non-empty bit string, i.e. the mapping from source symbols to bit strings is injective.- For example the mapping
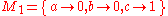 is not non-singular because both "a" and "b" map to the same bit string "0" ; any extension of this mapping will generate a lossy (non-lossless) coding. Such singular coding may still be useful when some loss of information is acceptable (for example when such code is used in audio or video compression, where a lossy coding becomes equivalent to source quantizationQuantization (signal processing)Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
is not non-singular because both "a" and "b" map to the same bit string "0" ; any extension of this mapping will generate a lossy (non-lossless) coding. Such singular coding may still be useful when some loss of information is acceptable (for example when such code is used in audio or video compression, where a lossy coding becomes equivalent to source quantizationQuantization (signal processing)Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
). - However, the mapping
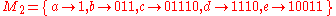 is non-singular ; its extension will generate a lossless coding, which will be useful for general data transmission (but this feature is not always required). Note that it is not necessary for the non-singular code to be more compact than the source (and in many applications, a larger code is useful, for example as a way to detect and/or recover from encoding or transmission errors, or in security applications to protect a source from undetectable tampering).
is non-singular ; its extension will generate a lossless coding, which will be useful for general data transmission (but this feature is not always required). Note that it is not necessary for the non-singular code to be more compact than the source (and in many applications, a larger code is useful, for example as a way to detect and/or recover from encoding or transmission errors, or in security applications to protect a source from undetectable tampering).
Uniquely decodable codes
A code is uniquely decodable if its extension is non-singular. Whether a given code is uniquely decodable can be decided with the Sardinas–Patterson algorithmSardinas–Patterson algorithm
In coding theory, the Sardinas–Patterson algorithm is a classical algorithm for determining whether a given variable-length code is uniquely decodable. The algorithm carries out a systematic search for a string which admits two different decompositions into codewords...
.
- The mapping
 is uniquely decodable (this can be demonstrated by looking at the follow-set after each target bit string in the map, because each bitstring is terminated as soon as we see a 0 bit which cannot follow any existing code to create a longer valid code in the map, but unambiguously starts a new code).
is uniquely decodable (this can be demonstrated by looking at the follow-set after each target bit string in the map, because each bitstring is terminated as soon as we see a 0 bit which cannot follow any existing code to create a longer valid code in the map, but unambiguously starts a new code). - Consider again the code
 from the previous section. This code, which is based on an example found in , is not uniquely decodable, since the string 011101110011 can be interpreted as the sequence of codewords 01110–1110 – 011, but also as the sequence of codewords 011 – 1 – 011 – 10011. Two possible decodings of this encoded string are thus given by cdb and babe. However, such a code is useful when the set of all possible source symbols is completely known and finite, or when there are restrictions (for example a formal syntax) that determine if source elements of this extension are acceptable. Such restrictions permit the decoding of the original message by checking which of the possible source symbols mapped to the same symbol are valid under those restrictions.
from the previous section. This code, which is based on an example found in , is not uniquely decodable, since the string 011101110011 can be interpreted as the sequence of codewords 01110–1110 – 011, but also as the sequence of codewords 011 – 1 – 011 – 10011. Two possible decodings of this encoded string are thus given by cdb and babe. However, such a code is useful when the set of all possible source symbols is completely known and finite, or when there are restrictions (for example a formal syntax) that determine if source elements of this extension are acceptable. Such restrictions permit the decoding of the original message by checking which of the possible source symbols mapped to the same symbol are valid under those restrictions.
Prefix codes
A code is a prefix code if no target bit string in the mapping is a prefix of the target bit string of a different source symbol in the same mapping. This means that symbols can be decoded instantaneously after their entire codeword is received. Other commonly used names for this concept are prefix-free code, instantaneous code, or context-free code.- The example mapping
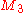 in the previous paragraph is not a prefix code because we don't know after reading the bit string "0" if it encodes a "a" source symbol, or if it is the prefix of the encodings of the "b" or "c" symbols.
in the previous paragraph is not a prefix code because we don't know after reading the bit string "0" if it encodes a "a" source symbol, or if it is the prefix of the encodings of the "b" or "c" symbols. - An example of a prefix code is shown below.
Symbol Codeword a 0 b 10 c 110 d 111
-
- Example of encoding and decoding:
- aabacda → 001001101110 → |0|0|10|0|110|111|0| → aabacda
- Example of encoding and decoding:
A special case of prefix codes are block code
Block code
In coding theory, block codes refers to the large and important family of error-correcting codes that encode data in blocks.There is a vast number of examples for block codes, many of which have a wide range of practical applications...
s. Here all codewords must have the same length. The latter are not very useful in the context of source coding
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
, but often serve as error correcting codes
Forward error correction
In telecommunication, information theory, and coding theory, forward error correction or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels....
in the context of channel coding.
Advantages
The advantage of a variable-length code is that unlikely source symbols can be assigned longer codewords and likely source symbols can be assigned shorter codewords, thus giving a low expectedExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
codeword length. For the above example, if the probabilities of (a, b, c, d) were
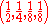 , the expected number of bits used to represent a source symbol using the code above would be:
, the expected number of bits used to represent a source symbol using the code above would be:
-
-
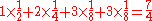 .
.
-
As the entropy of this source is 1.7500 bits per symbol, this code compresses the source as much as possible so that the source can be recovered with zero error.

