
Sardinas–Patterson algorithm
Encyclopedia
In coding theory
, the Sardinas–Patterson algorithm is a classical algorithm for determining whether a given variable-length code
is uniquely decodable. The algorithm carries out a systematic search for a string which admits two different decompositions into codewords. As Knuth reports, the algorithm was rediscovered about ten years later in 1963 by Floyd
, despite the fact that it was at the time already well known in coding theory.
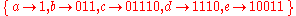 . This code, which is based on an example by Berstel, is an example of a code which is not uniquely decodable, since the string
. This code, which is based on an example by Berstel, is an example of a code which is not uniquely decodable, since the string
can be interpreted as the sequence of codewords
but also as the sequence of codewords
Two possible decodings of this encoded string are thus given by cdb and babe.
In general, a codeword can be found by the following idea: In the first round, we choose two codewords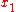 and
and 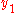 such that
such that 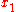 is a prefix
is a prefix
of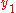 , that is,
, that is,
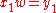 for some "dangling suffix"
for some "dangling suffix"  . If one tries first
. If one tries first  and
and 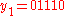 , the dangling suffix
, the dangling suffix
is . If we manage to find two sequences
. If we manage to find two sequences  and
and  of codewords such that
of codewords such that
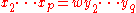 , then we are finished: For then the string
, then we are finished: For then the string 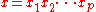 can alternatively be decomposed as
can alternatively be decomposed as  , and we have found the desired string having at least two different decompositions into codewords. In the second round, we try out two different approaches: the first trial is to look for a codeword that has w as prefix. Then we obtain a new dangling suffix w, with which we can continue our search. If we eventually encounter a dangling suffix that is itself a codeword (or the empty word), then the search will terminate, as we know there exists a string with two decompositions. The second trial is to seek for a codeword that is itself a prefix of w. In our example, we have
, and we have found the desired string having at least two different decompositions into codewords. In the second round, we try out two different approaches: the first trial is to look for a codeword that has w as prefix. Then we obtain a new dangling suffix w, with which we can continue our search. If we eventually encounter a dangling suffix that is itself a codeword (or the empty word), then the search will terminate, as we know there exists a string with two decompositions. The second trial is to seek for a codeword that is itself a prefix of w. In our example, we have  , and the sequence 1 is a codeword. We can thus also continue with w'=0 as the new dangling suffix.
, and the sequence 1 is a codeword. We can thus also continue with w'=0 as the new dangling suffix.
s. In general, for two sets of strings D and N, the (left) quotient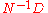 is defined as the residual words obtained from D by removing some prefix in N. Formally,
is defined as the residual words obtained from D by removing some prefix in N. Formally, 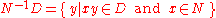 . Now let
. Now let  denote the (finite) set of codewords in the given code.
denote the (finite) set of codewords in the given code.
The algorithm proceeds in rounds, where we maintain in each round not only one dangling suffix as described above, but the (finite) set of all potential dangling suffixes. Starting with round , the set of potential dangling suffixes will be denoted by
, the set of potential dangling suffixes will be denoted by 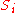 . The sets
. The sets 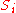 are defined inductively
are defined inductively
as follows:
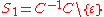 . Here, the symbol
. Here, the symbol  denotes the empty word.
denotes the empty word.
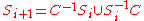 , for all
, for all 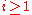 .
.
The algorithm computes the sets in increasing order of
in increasing order of 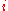 . As soon as one of the
. As soon as one of the 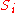 contains a word from C or the empty word, then the algorithm terminates and answers that the given code is not uniquely decodable. Otherwise, once a set
contains a word from C or the empty word, then the algorithm terminates and answers that the given code is not uniquely decodable. Otherwise, once a set 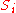
equals a previously encountered set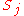 with
with  , then the algorithm would enter in principle an endless loop. Instead of continuing endlessly, it answers that the given code is uniquely decodable.
, then the algorithm would enter in principle an endless loop. Instead of continuing endlessly, it answers that the given code is uniquely decodable.
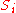 are sets of suffixes of a finite set of codewords, there are only finitely many different candidates for
are sets of suffixes of a finite set of codewords, there are only finitely many different candidates for 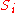 . Since visiting one of the sets for the second time will cause the algorithm to stop, the algorithm cannot continue endlessly and thus must always terminate
. Since visiting one of the sets for the second time will cause the algorithm to stop, the algorithm cannot continue endlessly and thus must always terminate
. A proof that the algorithm is correct, i.e. that it always gives the correct answer, is found in the textbooks by Salomaa
and by Berstel et al.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, the Sardinas–Patterson algorithm is a classical algorithm for determining whether a given variable-length code
Variable-length code
In coding theory a variable-length code is a code which maps source symbols to a variable number of bits.Variable-length codes can allow sources to be compressed and decompressed with zero error and still be read back symbol by symbol...
is uniquely decodable. The algorithm carries out a systematic search for a string which admits two different decompositions into codewords. As Knuth reports, the algorithm was rediscovered about ten years later in 1963 by Floyd
Robert Floyd
Robert W Floyd was an eminent computer scientist.His contributions include the design of the Floyd–Warshall algorithm , which efficiently finds all shortest paths in a graph, Floyd's cycle-finding algorithm for detecting cycles in a sequence, and his work on parsing...
, despite the fact that it was at the time already well known in coding theory.
Idea of the algorithm
Consider the code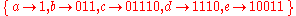 . This code, which is based on an example by Berstel, is an example of a code which is not uniquely decodable, since the string
. This code, which is based on an example by Berstel, is an example of a code which is not uniquely decodable, since the string- 011101110011
can be interpreted as the sequence of codewords
- 01110 – 1110 – 011,
but also as the sequence of codewords
- 011 – 1 – 011 – 10011.
Two possible decodings of this encoded string are thus given by cdb and babe.
In general, a codeword can be found by the following idea: In the first round, we choose two codewords
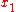 and
and 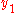 such that
such that 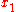 is a prefix
is a prefixPrefix
A prefix is an affix which is placed before the root of a word. Particularly in the study of languages,a prefix is also called a preformative, because it alters the form of the words to which it is affixed.Examples of prefixes:...
of
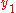 , that is,
, that is,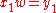 for some "dangling suffix"
for some "dangling suffix"  . If one tries first
. If one tries first  and
and 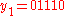 , the dangling suffix
, the dangling suffixSuffix
In linguistics, a suffix is an affix which is placed after the stem of a word. Common examples are case endings, which indicate the grammatical case of nouns or adjectives, and verb endings, which form the conjugation of verbs...
is
 . If we manage to find two sequences
. If we manage to find two sequences  and
and  of codewords such that
of codewords such that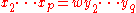 , then we are finished: For then the string
, then we are finished: For then the string 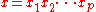 can alternatively be decomposed as
can alternatively be decomposed as  , and we have found the desired string having at least two different decompositions into codewords. In the second round, we try out two different approaches: the first trial is to look for a codeword that has w as prefix. Then we obtain a new dangling suffix w, with which we can continue our search. If we eventually encounter a dangling suffix that is itself a codeword (or the empty word), then the search will terminate, as we know there exists a string with two decompositions. The second trial is to seek for a codeword that is itself a prefix of w. In our example, we have
, and we have found the desired string having at least two different decompositions into codewords. In the second round, we try out two different approaches: the first trial is to look for a codeword that has w as prefix. Then we obtain a new dangling suffix w, with which we can continue our search. If we eventually encounter a dangling suffix that is itself a codeword (or the empty word), then the search will terminate, as we know there exists a string with two decompositions. The second trial is to seek for a codeword that is itself a prefix of w. In our example, we have  , and the sequence 1 is a codeword. We can thus also continue with w'=0 as the new dangling suffix.
, and the sequence 1 is a codeword. We can thus also continue with w'=0 as the new dangling suffix.Precise description of the algorithm
The algorithm is described most conveniently using quotients of formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s. In general, for two sets of strings D and N, the (left) quotient
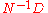 is defined as the residual words obtained from D by removing some prefix in N. Formally,
is defined as the residual words obtained from D by removing some prefix in N. Formally, 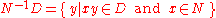 . Now let
. Now let  denote the (finite) set of codewords in the given code.
denote the (finite) set of codewords in the given code.The algorithm proceeds in rounds, where we maintain in each round not only one dangling suffix as described above, but the (finite) set of all potential dangling suffixes. Starting with round
 , the set of potential dangling suffixes will be denoted by
, the set of potential dangling suffixes will be denoted by 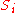 . The sets
. The sets 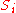 are defined inductively
are defined inductivelyRecursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
as follows:
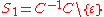 . Here, the symbol
. Here, the symbol  denotes the empty word.
denotes the empty word.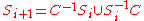 , for all
, for all 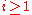 .
.The algorithm computes the sets
 in increasing order of
in increasing order of 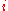 . As soon as one of the
. As soon as one of the 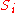 contains a word from C or the empty word, then the algorithm terminates and answers that the given code is not uniquely decodable. Otherwise, once a set
contains a word from C or the empty word, then the algorithm terminates and answers that the given code is not uniquely decodable. Otherwise, once a set 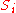
equals a previously encountered set
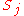 with
with  , then the algorithm would enter in principle an endless loop. Instead of continuing endlessly, it answers that the given code is uniquely decodable.
, then the algorithm would enter in principle an endless loop. Instead of continuing endlessly, it answers that the given code is uniquely decodable.Termination and correctness of the algorithm
Since all sets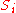 are sets of suffixes of a finite set of codewords, there are only finitely many different candidates for
are sets of suffixes of a finite set of codewords, there are only finitely many different candidates for 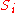 . Since visiting one of the sets for the second time will cause the algorithm to stop, the algorithm cannot continue endlessly and thus must always terminate
. Since visiting one of the sets for the second time will cause the algorithm to stop, the algorithm cannot continue endlessly and thus must always terminateTerminate
Terminate was a shareware modem terminal and host program for MS-DOS and compatible operating systems developed from the early to the late 1990s by the Dane Bo Bendtsen...
. A proof that the algorithm is correct, i.e. that it always gives the correct answer, is found in the textbooks by Salomaa
Arto Salomaa
Arto Salomaa is a Finnish mathematician andcomputer scientist. His research career, which spans over forty years,is focused on formal languages and automata theory.A 2004 citation stated that...
and by Berstel et al.
See also
- Kraft's inequalityKraft's inequalityIn coding theory, Kraft's inequality, named after Leon Kraft, gives a necessary and sufficient condition for the existence of a uniquely decodable code for a given set of codeword lengths...
in some cases provides a quick way to exclude the possibility that a given code is uniquely decodable. - Prefix codePrefix codeA prefix code is a type of code system distinguished by its possession of the "prefix property"; which states that there is no valid code word in the system that is a prefix of any other valid code word in the set...
s and block codeBlock codeIn coding theory, block codes refers to the large and important family of error-correcting codes that encode data in blocks.There is a vast number of examples for block codes, many of which have a wide range of practical applications...
s are important classes of codes which are uniquely decodable by definition. - Timeline of information theoryTimeline of information theoryA timeline of events related to information theory, quantum information theory, data compression, error correcting codes and related subjects....

