V-statistic
Encyclopedia
V-statistics are a class of statistics named for Richard von Mises who developed their asymptotic distribution theory
in a fundamental paper in 1947. V-statistics are closely related to U-statistic
s (U for “unbiased
”) introduced by Wassily Hoeffding
in 1948. A V-statistic is a statistical function (of a sample) defined by a particular statistical functional of a probability distribution.
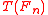of the empirical distribution function
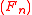are called statistical functions. Differentiability
of the functional T plays a key role in the von Mises approach; thus von Mises considers differentiable statistical functionals.
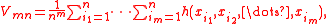
where h is a symmetric kernel function. Serfling discusses how to find the kernel in practice. Vmn is called a V-statistic of degree m.
A symmetric kernel of degree 2 is a function h(x, y), such that h(x, y) = h(y, x) for all x and y in the domain of h. For samples x1, ..., xn, the corresponding V-statistic is defined
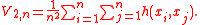
of the statistic is different: in (1) it is normal, in (2) it is chi-squared, and in (3) it is a weighted sum of chi-squared variables.
Von Mises' approach is a unifying theory that covers all of the cases above. Informally, the type of asymptotic distribution
of a statistical function depends on the order of "degeneracy," which is determined by which term is the first non-vanishing term in the Taylor expansion
of the functional T. In case it is the linear term, the limit distribution is normal; otherwise higher order types of distributions arise (under suitable conditions such that a central limit theorem holds).
There are a hierarchy of cases parallel to asymptotic theory of U-statistic
s. Let A(m) be the property defined by:
Case m = 1 (Non-degenerate kernel):
If A(1) is true, the statistic is a sample mean and the Central Limit Theorem
implies that T(Fn) is asymptotically normal.
In the variance example (4), m2 is asymptotically normal with mean
and variance 
, where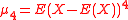 
.
Case m = 2 (Degenerate kernel):
Suppose A(2) is true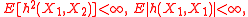, and
and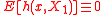 
. Then nV2,n converges in distribution to a weighted sum of independent chi-squared variables:
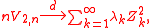
where
are independent standard normal variables and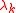 
are constants that depend on the distribution F and the functional T. In this case the asymptotic distribution
is called a quadratic form of centered Gaussian random variables. The statistic V2,n is called a degenerate kernel V-statistic. The V-statistic associated with the Cramer–von Mises functional (Example 3) is an example of a degenerate kernel V-statistic.
Asymptotic theory
Asymptotic theory or large sample theory is the branch of mathematics which studies properties of asymptotic expansions.The most known result of this field is the prime number theorem:...
in a fundamental paper in 1947. V-statistics are closely related to U-statistic
U-statistic
In statistical theory, a U-statistic is a class of statistics that is especially important in estimation theory. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimators...
s (U for “unbiased
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
”) introduced by Wassily Hoeffding
Wassily Hoeffding
Wassily Hoeffding was an American statistician and probabilist...
in 1948. A V-statistic is a statistical function (of a sample) defined by a particular statistical functional of a probability distribution.
Statistical functions
Statistics that can be represented as functionals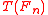 of the empirical distribution functionEmpirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
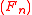are called statistical functions. DifferentiabilityDifferentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
of the functional T plays a key role in the von Mises approach; thus von Mises considers differentiable statistical functionals.
Examples of statistical functions
The k-th central momentCentral momentIn probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
is the functional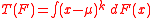
, where 
is the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of X. The associated statistical function is the sample k-th central moment,
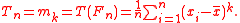
The chi-squared goodness-of-fitPearson's chi-squared testPearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
statistic is a statistical function T(Fn), corresponding to the statistical functional
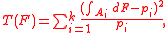
where Ai are the k cells and pi are the specified probabilities of the cells under the null hypothesis.
The Cramér–von-Mises and Anderson–Darling goodness-of-fit statistics are based on the functional
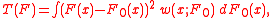
where w(x; F0) is a specified weight function and F0 is a specified null distribution. If w is the identity function then T(Fn) is the well known Cramér–von-Mises goodness-of-fit statistic; if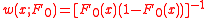
then T(Fn) is the Anderson–Darling statistic.
Representation as a V-statistic
Suppose x1, ..., xn is a sample. In typical applications the statistical function has a representation as the V-statistic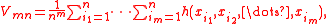where h is a symmetric kernel function. Serfling discusses how to find the kernel in practice. Vmn is called a V-statistic of degree m.
A symmetric kernel of degree 2 is a function h(x, y), such that h(x, y) = h(y, x) for all x and y in the domain of h. For samples x1, ..., xn, the corresponding V-statistic is defined
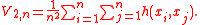
Example of a V-statistic
An example of a degree-2 V-statistic is the second central momentCentral momentIn probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
m2.
If h(x, y) = (x − y)2/2, the corresponding V-statistic is
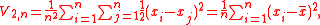
which is the maximum likelihood estimator of variance. With the same kernel, the corresponding U-statisticU-statisticIn statistical theory, a U-statistic is a class of statistics that is especially important in estimation theory. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimators...
is the (unbiased) sample variance:
.
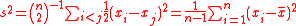Asymptotic distribution
In examples 1–3, the asymptotic distributionAsymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
of the statistic is different: in (1) it is normal, in (2) it is chi-squared, and in (3) it is a weighted sum of chi-squared variables.
Von Mises' approach is a unifying theory that covers all of the cases above. Informally, the type of asymptotic distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
of a statistical function depends on the order of "degeneracy," which is determined by which term is the first non-vanishing term in the Taylor expansion
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of the functional T. In case it is the linear term, the limit distribution is normal; otherwise higher order types of distributions arise (under suitable conditions such that a central limit theorem holds).
There are a hierarchy of cases parallel to asymptotic theory of U-statistic
U-statistic
In statistical theory, a U-statistic is a class of statistics that is especially important in estimation theory. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimators...
s. Let A(m) be the property defined by:
- A(m):
- Var(h(X1, ..., Xk)) = 0 for k < m, and Var(h(X1, ..., Xk)) > 0 for k = m;
- nm/2Rmn tends to zero (in probability). (Rmn is the remainder term in the Taylor series for T.)
Case m = 1 (Non-degenerate kernel):
If A(1) is true, the statistic is a sample mean and the Central Limit Theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
implies that T(Fn) is asymptotically normal.
In the variance example (4), m2 is asymptotically normal with mean
and variance , where 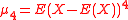.Case m = 2 (Degenerate kernel):
Suppose A(2) is true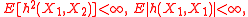, and
and 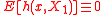. Then nV2,n converges in distribution to a weighted sum of independent chi-squared variables: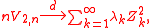where
are independent standard normal variables and 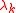are constants that depend on the distribution F and the functional T. In this case the asymptotic distributionAsymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
is called a quadratic form of centered Gaussian random variables. The statistic V2,n is called a degenerate kernel V-statistic. The V-statistic associated with the Cramer–von Mises functional (Example 3) is an example of a degenerate kernel V-statistic.