
Ultrafinitism
Encyclopedia
In the philosophy of mathematics
, ultrafinitism, also known as ultraintuitionism, strict-finitism, actualism, and strong-finitism is a form of finitism
. There are various philosophies of mathematics which are called ultrafinitism. One of major identifying properties common between most of these philosophies is their denial of totality of number theoretic functions like exponentiation over natural numbers.
, ultrafinitists deny the existence of the infinite set N of natural numbers, on the grounds that it can never be completed.
In addition, some ultrafinitists are concerned with our own physical restrictions in constructing (even finite) mathematical objects.
Thus some ultrafinitists will deny the existence of, for example, the floor
of the first Skewes' number, which is a huge number defined using the exponential function
as exp(exp(exp(79))), or
The reason is that nobody has yet calculated what natural number
is the floor of this real number
, and it may not even be physically possible to do so.
Similarly,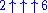 is considered only a formal expression which does not correspond to a natural number.
is considered only a formal expression which does not correspond to a natural number.
The ultrafinism concerned with physical realizability of mathematics is often called actualism.
Edward Nelson
criticizes the classical conception of natural numbers because of the circularity of its definition. In classical mathematics the natural numbers are defined as 0 and numbers obtained by the iterative applications of the successor function to 0. But the concept of natural number is already assumed for the iteration. In other words, to obtain a number like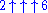 one needs to perform the successor function iteratively, in fact exactly
one needs to perform the successor function iteratively, in fact exactly 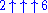 times to 0.
times to 0.
Some versions of ultrafinitism are forms of constructivism
, but even constructivists generally view the philosophy as unworkably extreme.
The logical foundation of ultrafinitism is unclear; in his comprehensive survey Constructivism in Mathematics (1988), the constructive logician A. S. Troelstra
dismissed it by saying "no satisfactory development exists at present." This was not so much a philosophical objection as it was an admission that, in a rigorous work of mathematical logic
, there was simply nothing precise enough to include.
. Other mathematicians who have worked in the topic include Doron Zeilberger
, Edward Nelson
, and Rohit Jivanlal Parikh
. The philosophy is also sometimes associated with the views of Ludwig Wittgenstein
, Robin Gandy
and J. Hjelmslev.
Shaughan Lavine has developed a form of set-theoretical ultra-finitism that is consistent with classical mathematics.
, as in Andras Kornai
's work on explicit finitism (which does not deny the existence of large numbers) and
Vladimir Sazonov's notion of feasible number.
There has been considerable formal development on complexity based views like Samuel Buss
's Bounded Arithmetic theories which capture mathematics associated with various complexity classes like P
and PSPACE
. The power of these theories for developing mathematics is studied in Bounded Reverse Mathematics as can be found in the works of Stephen A. Cook and Phuong The Nguyen. However these researches are not philosophies of mathematics but rather the study of restricted forms of reasoning similar to Reverse Mathematics
.
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
, ultrafinitism, also known as ultraintuitionism, strict-finitism, actualism, and strong-finitism is a form of finitism
Finitism
In the philosophy of mathematics, one of the varieties of finitism is an extreme form of constructivism, according to which a mathematical object does not exist unless it can be constructed from natural numbers in a finite number of steps...
. There are various philosophies of mathematics which are called ultrafinitism. One of major identifying properties common between most of these philosophies is their denial of totality of number theoretic functions like exponentiation over natural numbers.
Main ideas
Like other strict finitistsFinitism
In the philosophy of mathematics, one of the varieties of finitism is an extreme form of constructivism, according to which a mathematical object does not exist unless it can be constructed from natural numbers in a finite number of steps...
, ultrafinitists deny the existence of the infinite set N of natural numbers, on the grounds that it can never be completed.
In addition, some ultrafinitists are concerned with our own physical restrictions in constructing (even finite) mathematical objects.
Thus some ultrafinitists will deny the existence of, for example, the floor
Floor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
of the first Skewes' number, which is a huge number defined using the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
as exp(exp(exp(79))), or
The reason is that nobody has yet calculated what natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
is the floor of this real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, and it may not even be physically possible to do so.
Similarly,
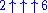 is considered only a formal expression which does not correspond to a natural number.
is considered only a formal expression which does not correspond to a natural number.The ultrafinism concerned with physical realizability of mathematics is often called actualism.
Edward Nelson
Edward Nelson
Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...
criticizes the classical conception of natural numbers because of the circularity of its definition. In classical mathematics the natural numbers are defined as 0 and numbers obtained by the iterative applications of the successor function to 0. But the concept of natural number is already assumed for the iteration. In other words, to obtain a number like
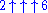 one needs to perform the successor function iteratively, in fact exactly
one needs to perform the successor function iteratively, in fact exactly 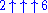 times to 0.
times to 0.Some versions of ultrafinitism are forms of constructivism
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
, but even constructivists generally view the philosophy as unworkably extreme.
The logical foundation of ultrafinitism is unclear; in his comprehensive survey Constructivism in Mathematics (1988), the constructive logician A. S. Troelstra
A. S. Troelstra
Anne Sjerp Troelstra is Emeritus professor of pure mathematics and foundations of mathematics at the Institute for Logic, Language and Computation of the University of Amsterdam....
dismissed it by saying "no satisfactory development exists at present." This was not so much a philosophical objection as it was an admission that, in a rigorous work of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, there was simply nothing precise enough to include.
People associated with ultrafinitism
Serious work on ultrafinitism has been led, since 1959, by Alexander Esenin-VolpinAlexander Esenin-Volpin
Alexander Sergeyevich Esenin-Volpin is a prominent Russian-American poet and mathematician.Born on May 12, 1924 in the former Soviet Union, he was a notable dissident, political prisoner, poet, and mathematician...
. Other mathematicians who have worked in the topic include Doron Zeilberger
Doron Zeilberger
Doron Zeilberger is an Israeli mathematician, known for his work in combinatorics.He is a Board of Governors Professor of Mathematics at Rutgers University...
, Edward Nelson
Edward Nelson
Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...
, and Rohit Jivanlal Parikh
Rohit Jivanlal Parikh
Rohit Jivanlal Parikh , is a mathematician, logician, and philosopher who has worked in many areas in traditional logic, including recursion theory and proof theory...
. The philosophy is also sometimes associated with the views of Ludwig Wittgenstein
Ludwig Wittgenstein
Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947...
, Robin Gandy
Robin Gandy
Robin Oliver Gandy was a British mathematician and logician.He was a friend, student, and associate of Alan Turing, having been supervised by Turing during his PhD at the University of Cambridge , where they worked together.Educated at Abbotsholme, Robin Gandy took two years of the Mathematical...
and J. Hjelmslev.
Shaughan Lavine has developed a form of set-theoretical ultra-finitism that is consistent with classical mathematics.
Complexity theory based restrictions
Other considerations of the possibility of avoiding unwieldily large numbers can be based on computational complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, as in Andras Kornai
Andras Kornai
András Kornai is a well-known mathematical linguist. He earned his mathematics PhD in 1983 from Eötvös Loránd University, Budapest where his advisor was Miklós Ajtai...
's work on explicit finitism (which does not deny the existence of large numbers) and
Vladimir Sazonov's notion of feasible number.
There has been considerable formal development on complexity based views like Samuel Buss
Samuel Buss
Samuel R. Buss is a American computer scientist and mathematician who has made major contributions to the fields of mathematical logic, complexity theory and proof complexity...
's Bounded Arithmetic theories which capture mathematics associated with various complexity classes like P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
and PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
. The power of these theories for developing mathematics is studied in Bounded Reverse Mathematics as can be found in the works of Stephen A. Cook and Phuong The Nguyen. However these researches are not philosophies of mathematics but rather the study of restricted forms of reasoning similar to Reverse Mathematics
Reverse mathematics
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
.
External links
- Explicit finitism by Andras KornaiAndras KornaiAndrás Kornai is a well-known mathematical linguist. He earned his mathematics PhD in 1983 from Eötvös Loránd University, Budapest where his advisor was Miklós Ajtai...
- On feasible numbers (http://www.csc.liv.ac.uk/~sazonov/papers/lcc.ps) by Vladimir Sazonov
- "Real" Analysis Is A Degenerate Case Of Discrete Analysis by Doron ZeilbergerDoron ZeilbergerDoron Zeilberger is an Israeli mathematician, known for his work in combinatorics.He is a Board of Governors Professor of Mathematics at Rutgers University...
- Discussion on formal foundations on MathOverflow
- History of constructivism in the 20th century by A. S. TroelstraA. S. TroelstraAnne Sjerp Troelstra is Emeritus professor of pure mathematics and foundations of mathematics at the Institute for Logic, Language and Computation of the University of Amsterdam....
- Predicative Arithmetic by Edward NelsonEdward NelsonEdward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...
- Logical Foundations of Proof Complexity by Stephen A. Cook and Phuong The Nguyen
- Bounded Reverse Mathematics by Phuong The Nguyen


