U-chart
Encyclopedia
{mn}
| meanlimits =
| meanstatistic =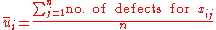
}}
In statistical quality control
, the u-chart is a type of control chart
used to monitor "count"-type data where the sample size is greater than one, typically the average number of nonconformities per unit.
The u-chart differs from the c-chart in that it accounts for the possibility that the number or size of inspection units for which nonconformities are to be counted may vary. Larger samples may be an economic necessity or may be necessary to increase the area of opportunity in order to track very low nonconformity levels.
Examples of processes suitable for monitoring with a u-chart include:
As with the c-chart, the Poisson distribution
is the basis for the chart and requires the same assumptions.
The control limits for this chart type are
where 
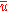is the estimate of the long-term process mean established during control-chart setup. The observations 
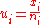are plotted against these control limits, where xi is the number of nonconformities for the ith subgroup and ni is the number of inspection units in the ith subgroup.
| meanlimits =
| meanstatistic =
}}
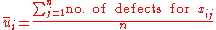
In statistical quality control
Statistical process control
Statistical process control is the application of statistical methods to the monitoring and control of a process to ensure that it operates at its full potential to produce conforming product. Under SPC, a process behaves predictably to produce as much conforming product as possible with the least...
, the u-chart is a type of control chart
Control chart
Control charts, also known as Shewhart charts or process-behaviour charts, in statistical process control are tools used to determine whether or not a manufacturing or business process is in a state of statistical control.- Overview :...
used to monitor "count"-type data where the sample size is greater than one, typically the average number of nonconformities per unit.
The u-chart differs from the c-chart in that it accounts for the possibility that the number or size of inspection units for which nonconformities are to be counted may vary. Larger samples may be an economic necessity or may be necessary to increase the area of opportunity in order to track very low nonconformity levels.
Examples of processes suitable for monitoring with a u-chart include:
- Monitoring the number of nonconformities per lot of raw material received where the lot size varies
- Monitoring the number of new infections in a hospital per day
- Monitoring the number of accidents for delivery trucks per day
As with the c-chart, the Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
is the basis for the chart and requires the same assumptions.
The control limits for this chart type are
where 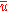is the estimate of the long-term process mean established during control-chart setup. The observations 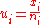are plotted against these control limits, where xi is the number of nonconformities for the ith subgroup and ni is the number of inspection units in the ith subgroup.