Programming language for Computable Functions
Encyclopedia
In computer science
, Programming Computable Functions,"PCF is a programming language for computable functions, based on LCF, Scott’s logic of computable functions" . Programming Computable Functions is used by . It is also referred to as Programming with Computable Functions or Programming language for Computable Functions. or PCF, is a typed
functional language
introduced by Gordon Plotkin
in 1977. It is based on the Logic of Computable Functions
(LCF) by Dana Scott
. It can be considered as an extended version of the typed lambda calculus
or a simplified version of modern typed functional languages such as ML
.
A fully abstract model for PCF was first given by Milner
(1977). However, since Milner's model was essentially based on the syntax of PCF it was considered less than satisfactory (Ong, 1995). The first two fully abstract models not employing syntax were formulated during the 1990s. These models are based on game semantics
(Hyland and Ong, 2000; Abramsky, Jagadeesan, and Malacaria, 2000) and Kripke logical relations (O'Hearn and Riecke, 1995). For a time it was felt that neither of these models was completely satisfactory, since they were not effectively presentable. However, Ralph Loader demonstrated that no effectively presentable fully abstract model could exist, since the question of program equivalence in the finitary fragment of PCF is not decidable.
A context is a list of pairs x : σ, where x is a variable name and σ is a type, such that no variable name is duplicated. One then defines typing judgments of terms-in-context in the usual way for the following syntactical constructs:
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, Programming Computable Functions,"PCF is a programming language for computable functions, based on LCF, Scott’s logic of computable functions" . Programming Computable Functions is used by . It is also referred to as Programming with Computable Functions or Programming language for Computable Functions. or PCF, is a typed
Type system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
functional language
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
introduced by Gordon Plotkin
Gordon Plotkin
Gordon D. Plotkin, FRS, FRSE is a Scottish computer scientist.Gordon Plotkin is best-known for his introduction of structural operational semantics and his work on denotational semantics. In particular, his notes on A Structural Approach to Operational Semantics of 1981 were very influential...
in 1977. It is based on the Logic of Computable Functions
Logic of Computable Functions
Logic of Computable Functions is a deductive system for computable functions proposed by Dana Scott in 1969 in an memorandum unpublished until 1993. It inspired:* Logic for Computable Functions , theorem proving logic by Robin Milner....
(LCF) by Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
. It can be considered as an extended version of the typed lambda calculus
Typed lambda calculus
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...
or a simplified version of modern typed functional languages such as ML
ML programming language
ML is a general-purpose functional programming language developed by Robin Milner and others in the early 1970s at the University of Edinburgh, whose syntax is inspired by ISWIM...
.
A fully abstract model for PCF was first given by Milner
Robin Milner
Arthur John Robin Gorell Milner FRS FRSE was a prominent British computer scientist.-Life, education and career:...
(1977). However, since Milner's model was essentially based on the syntax of PCF it was considered less than satisfactory (Ong, 1995). The first two fully abstract models not employing syntax were formulated during the 1990s. These models are based on game semantics
Game semantics
Game semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. In the late 1950s Paul Lorenzen was the...
(Hyland and Ong, 2000; Abramsky, Jagadeesan, and Malacaria, 2000) and Kripke logical relations (O'Hearn and Riecke, 1995). For a time it was felt that neither of these models was completely satisfactory, since they were not effectively presentable. However, Ralph Loader demonstrated that no effectively presentable fully abstract model could exist, since the question of program equivalence in the finitary fragment of PCF is not decidable.
Syntax
The types of PCF are inductively defined as- nat is a type
- For types σ and τ, there is a type σ → τ
A context is a list of pairs x : σ, where x is a variable name and σ is a type, such that no variable name is duplicated. One then defines typing judgments of terms-in-context in the usual way for the following syntactical constructs:
- Variables (if x : σ is part of a context Γ, then Γ ⊢ x : σ)
- Application (of a term of type σ → τ to a term of type σ)
- λ-abstraction
- The YY CombinatorY Combinator is an American seed-stage startup funding firm, started in March 2005. Y Combinator provides seed money, advice, and connections at two 3-month programs per year...
fixed point combinator (making terms of type σ out of terms of type σ → σ) - The successor (succ) and predecessor (pred) operations on nat and the constant 0
- The conditional if with the typing rule:
-
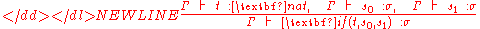
- (nats will be interpreted as booleans here with a convention like zero denoting truth, and any other number denoting falsity)
Denotational semantics
A relatively straightforward semantics for the language is the Scott model. In this model,
- Types are interpreted as certain domainsDomain theoryDomain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
.-
(the natural numbers with a bottom element adjoined, with the flat ordering) -
is interpreted as the domain of Scott-continuous functions from 
to 
-
- A context
is interpreted as the product 
- Terms in context
are interpreted as continuous functions 
- Variable terms are interpreted as projections
- Lambda abstraction and application are interpreted by making use of the cartesian closed structure of the category of domains and continuous functions
- Y is interpreted by taking the least fixed pointLeast fixed pointIn order theory, a branch of mathematics, the least fixed point of a function is the fixed point which is less than or equal to all other fixed points, according to some partial order....
of the argument
This model is not fully abstract for PCF; but it is fully abstract for the language obtained by adding a parallel or operator to PCF (p. 293 in the Hyland and Ong 2000 reference below).
External links