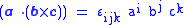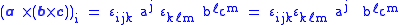Triple product
Encyclopedia
In mathematics
, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product.
 The scalar triple product (also called the mixed or box product) is defined as the dot product
The scalar triple product (also called the mixed or box product) is defined as the dot product
of one of the vectors with the cross product
of the other two.
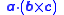
is the (signed) volume of the parallelepiped
defined by the three vectors given.
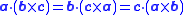
Switching the two vectors in the cross product negates the triple product, i.e.:
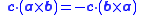 .
.
The parentheses may be omitted without causing ambiguity, since the dot product
cannot be evaluated first. If it were, it would leave the cross product of a scalar and a vector, which is not defined.
The scalar triple product can also be understood as the determinant
of the 3 × 3 matrix having the three vectors as its rows or columns (the determinant of a transposed matrix is the same as the original); this quantity is invariant under coordinate rotation.

Note that if the scalar triple product is equal to zero, then the three vectors a, b, and c are coplanar, since the "parallelepiped" defined by them would be flat and have no volume.
There is also this property of triple products: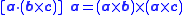
of the frame or the parity of the permutation of the vectors. This means the product is negated if the orientation is reversed, by for example by a parity transformation, and so is more properly described as a pseudoscalar
if the orientation can change.
This also relates to the handedness of the cross product; the cross product transforms as a pseudovector
under parity transformations and so is properly described as a pseudovector. The dot product of two vectors is a scalar but the dot product of a pseudovector and a vector is a pseudoscalar, so the scalar triple product must be pseudoscalar valued.
 In exterior algebra
In exterior algebra
and geometric algebra
the exterior product of two vectors is a bivector
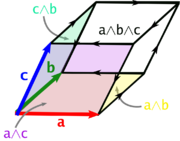
, while the exterior product of three vectors is a trivector. A bivector is an oriented plane element and a trivector is an oriented volume element, in the same way that a vector is an oriented line element. Given vectors a, b and c, the product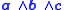
is a trivector with magnitude equal to the scalar triple product, and is the pseudoscalar dual of the triple product. As the exterior product is associative brackets are not needed as it does not matter which of or is calculated first, though the order of the vectors in the product does matter. Geometrically the trivector a ∧ b ∧ c corresponds to the parallelepiped spanned by a, b, and c, with bivectors , and matching the parallelogram faces of the parallelepiped.
of one vector with the cross product of the other two. The following relationships hold:

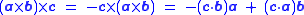 .
.
The first formula is known as triple product expansion, or Lagrange's formula,
although the latter name is ambiguous (see disambiguation page). Its right hand member is easier to remember by using the mnemonic
“BAC minus CAB”, provided one keeps in mind which vectors are dotted together. A proof is provided below.
These formulas are very useful in simplifying vector calculations in physics
. A related identity regarding gradient
s and useful in vector calculus is Lagrange's formula of vector cross-product identity: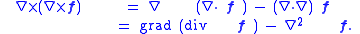
This can be also regarded as a special case of the more general Laplace-de Rham operator .
.
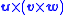 is given by:
is given by:
or
By adding and subtracting uxvxwx, this becomes
Similarly, the y and z components of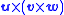 are given by:
are given by:
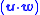 vy −
vy − 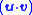 wy
wy
and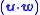 vz −
vz − 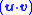 wz
wz
By combining these three components we obtain:
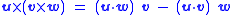
, the vector triple product is vector rather than pseudovector valued, as it is the product of a vector a and a pseudovector b × c. This can also be seen from the expansion in terms of the dot product, which consists only of a sum of vectors multiplied by scalars so must be vector valued.
, the triple product is
and
which can be simplified by performing a contraction on the Levi-Civita symbol
s, and simplifying the result.
and simplifying the result.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product.
Scalar triple product

Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of one of the vectors with the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of the other two.
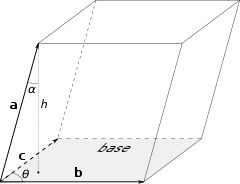
Geometric interpretation
Geometrically, the scalar triple product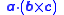
is the (signed) volume of the parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
defined by the three vectors given.
Properties
The scalar triple product can be evaluated numerically using any one of the following equivalent characterizations: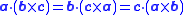
Switching the two vectors in the cross product negates the triple product, i.e.:
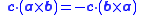 .
.The parentheses may be omitted without causing ambiguity, since the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
cannot be evaluated first. If it were, it would leave the cross product of a scalar and a vector, which is not defined.
The scalar triple product can also be understood as the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the 3 × 3 matrix having the three vectors as its rows or columns (the determinant of a transposed matrix is the same as the original); this quantity is invariant under coordinate rotation.

Note that if the scalar triple product is equal to zero, then the three vectors a, b, and c are coplanar, since the "parallelepiped" defined by them would be flat and have no volume.
There is also this property of triple products:
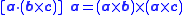
Scalar or pseudoscalar
Although the scalar triple product gives the volume of the parallelepiped it is the signed volume, the sign depending on the orientationOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of the frame or the parity of the permutation of the vectors. This means the product is negated if the orientation is reversed, by for example by a parity transformation, and so is more properly described as a pseudoscalar
Pseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
if the orientation can change.
This also relates to the handedness of the cross product; the cross product transforms as a pseudovector
Pseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
under parity transformations and so is properly described as a pseudovector. The dot product of two vectors is a scalar but the dot product of a pseudovector and a vector is a pseudoscalar, so the scalar triple product must be pseudoscalar valued.
As an exterior product

Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
and geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
the exterior product of two vectors is a bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
, while the exterior product of three vectors is a trivector. A bivector is an oriented plane element and a trivector is an oriented volume element, in the same way that a vector is an oriented line element. Given vectors a, b and c, the product
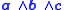
is a trivector with magnitude equal to the scalar triple product, and is the pseudoscalar dual of the triple product. As the exterior product is associative brackets are not needed as it does not matter which of or is calculated first, though the order of the vectors in the product does matter. Geometrically the trivector a ∧ b ∧ c corresponds to the parallelepiped spanned by a, b, and c, with bivectors , and matching the parallelogram faces of the parallelepiped.
Vector triple product
The vector triple product is defined as the cross productCross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of one vector with the cross product of the other two. The following relationships hold:

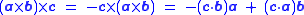 .
.The first formula is known as triple product expansion, or Lagrange's formula,
although the latter name is ambiguous (see disambiguation page). Its right hand member is easier to remember by using the mnemonic
Mnemonic
A mnemonic , or mnemonic device, is any learning technique that aids memory. To improve long term memory, mnemonic systems are used to make memorization easier. Commonly encountered mnemonics are often verbal, such as a very short poem or a special word used to help a person remember something,...
“BAC minus CAB”, provided one keeps in mind which vectors are dotted together. A proof is provided below.
These formulas are very useful in simplifying vector calculations in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. A related identity regarding gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
s and useful in vector calculus is Lagrange's formula of vector cross-product identity:
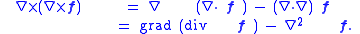
This can be also regarded as a special case of the more general Laplace-de Rham operator
 .
.Proof
The x component of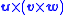 is given by:
is given by:- uy(vxwy − vywx) − uz(vzwx − vxwz)
or
- vx(uywy + uzwz) − wx(uyvy + uzvz)
By adding and subtracting uxvxwx, this becomes
- vx(uxwx + uywy + uzwz) − wx(uxvx + uyvy + uzvz) =
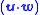 vx −
vx − 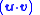 wx
wx
Similarly, the y and z components of
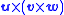 are given by:
are given by: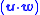 vy −
vy − 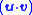 wy
wyand
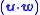 vz −
vz − 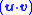 wz
wzBy combining these three components we obtain:
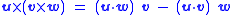
Vector or pseudovector
Where parity transformations need to be considered, so the cross product is treated as a pseudovectorPseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
, the vector triple product is vector rather than pseudovector valued, as it is the product of a vector a and a pseudovector b × c. This can also be seen from the expansion in terms of the dot product, which consists only of a sum of vectors multiplied by scalars so must be vector valued.
Notation
Using the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
, the triple product is
and
which can be simplified by performing a contraction on the Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
s,
 and simplifying the result.
and simplifying the result.