Trend stationary
Encyclopedia
In the statistical analysis
of time series
, a stochastic process
is trend stationary if any underlying trend can be removed
, leaving a stationary process
.
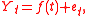
where t is time, f is any function mapping from the reals
to the reals, and {e} is a stationary process. The value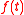
is said to be the trend value of the process at time t.
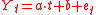
where t is time and et is an error term that is hypothesized to be white noise
or more generally to have been generated by any stationary process. Then one can uselinear regression
to obtain an estimate
of the true underlying trend slope 
and an estimate 
of the underlying intercept term b; if the estimate 
is significantly different from zero, this is sufficient to show with high confidence that the variable Y is non-stationary. The residuals
from this regression are given by
If these estimated residuals can be statistically shown to be stationary (more precisely, if one can reject the hypothesis that the true underlying errors are non-stationary), then the residuals are referred to as the detrended data, and the original series {Yt} is said to be trend stationary even though it is not stationary.
. For example, suppose that one hypothesizes that gross domestic product
is characterized by stationary deviations from a trend involving a constant growth rate. Then it could be modeled as
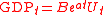
with Ut being hypothesized to be a stationary error process. To estimate the parameters
and B, one first takes the natural logarithm
(ln) of both sides of this equation:
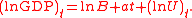
This log-linear equation is in the same form as the previous linear trend equation and can be detrended in the same way, giving the estimated
as the detrended value of 
, and hence the implied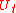 
as the detrended value of 
, assuming one can reject the hypothesis that 
is non-stationary.
This can be regressed linearly in the coefficients using t and t2 as regressors; again, if the residuals are shown to be stationary then they are the detrended values of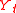
.
s but has all its other roots smaller than unity in magnitude.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
of time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
, a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
is trend stationary if any underlying trend can be removed
Trend estimation
Trend estimation is a statistical technique to aid interpretation of data. When a series of measurements of a process are treated as a time series, trend estimation can be used to make and justify statements about tendencies in the data...
, leaving a stationary process
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
.
Formal definition
A process {Y} is said to be trend stationary if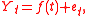where t is time, f is any function mapping from the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
to the reals, and {e} is a stationary process. The value
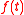is said to be the trend value of the process at time t.Simplest example: stationarity around a linear trend
Suppose the variable Y evolves according to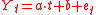where t is time and et is an error term that is hypothesized to be white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
or more generally to have been generated by any stationary process. Then one can uselinear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
to obtain an estimate
of the true underlying trend slope and an estimate of the underlying intercept term b; if the estimate is significantly different from zero, this is sufficient to show with high confidence that the variable Y is non-stationary. The residualsErrors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
from this regression are given by
If these estimated residuals can be statistically shown to be stationary (more precisely, if one can reject the hypothesis that the true underlying errors are non-stationary), then the residuals are referred to as the detrended data, and the original series {Yt} is said to be trend stationary even though it is not stationary.
Exponential growth trend
Many economic time series are characterized by exponential growthExponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
. For example, suppose that one hypothesizes that gross domestic product
Gross domestic product
Gross domestic product refers to the market value of all final goods and services produced within a country in a given period. GDP per capita is often considered an indicator of a country's standard of living....
is characterized by stationary deviations from a trend involving a constant growth rate. Then it could be modeled as
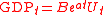
with Ut being hypothesized to be a stationary error process. To estimate the parameters
and B, one first takes the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
(ln) of both sides of this equation:
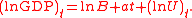
This log-linear equation is in the same form as the previous linear trend equation and can be detrended in the same way, giving the estimated
as the detrended value of , and hence the implied 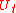as the detrended value of , assuming one can reject the hypothesis that is non-stationary.Quadratic trend
Trends do not have to be linear or log-linear. For example, a variable could have a quadratic trend:This can be regressed linearly in the coefficients using t and t2 as regressors; again, if the residuals are shown to be stationary then they are the detrended values of
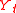.Other non-stationary processes that are not trend stationary but can be rendered stationary
Trend stationary processes are not the only kind of non-stationary process that can be transformed into a stationary one; another prominent such process exhibits one or more unit rootUnit root
In time series models in econometrics , a unit root is a feature of processes that evolve through time that can cause problems in statistical inference if it is not adequately dealt with....
s but has all its other roots smaller than unity in magnitude.