
Transversal
Encyclopedia
In geometry when two coplanar lines exist such that a third coplanar line passes thru both lines. This third line is named the Transversal.
In combinatorial
mathematics, given a collection C of sets
, a transversal is a set containing exactly one element from each member of the collection: it is a section
of the quotient map induced by the collection. If the original sets are not disjoint, there are several different definitions. One variation is that there is a bijection
f from the transversal to C such that x is an element of f(x) for each x in the transversal. Then the set is also called a system of distinct representatives. A less restrictive definition requires that the transversal just has a non-empty intersection with each member of C.
A partial transversal is a set containing at most one element from each member of the collection, or a set with an injection from the set to C.
in group theory
, given a subgroup
H of a group G, a right (respectively left) transversal is a set containing exactly one element from each right (respectively left) coset
of H.
Given a direct product of groups
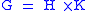 , then H is a transversal for the cosets of K.
, then H is a transversal for the cosets of K.
In combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics, given a collection C of sets
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a transversal is a set containing exactly one element from each member of the collection: it is a section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of the quotient map induced by the collection. If the original sets are not disjoint, there are several different definitions. One variation is that there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
f from the transversal to C such that x is an element of f(x) for each x in the transversal. Then the set is also called a system of distinct representatives. A less restrictive definition requires that the transversal just has a non-empty intersection with each member of C.
A partial transversal is a set containing at most one element from each member of the collection, or a set with an injection from the set to C.
Examples
As an example of the disjoint-sets meaning of transversal,in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, given a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H of a group G, a right (respectively left) transversal is a set containing exactly one element from each right (respectively left) coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of H.
Given a direct product of groups
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
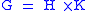 , then H is a transversal for the cosets of K.
, then H is a transversal for the cosets of K.- The marriage theoremMarriage theoremIn mathematics, Hall's marriage theorem is a combinatorial result that gives the condition allowing the selection of a distinct element from each of a collection of finite sets...
gives necessary and sufficient conditions for possibly overlapping subsets to have a transversal.

