
Transfer matrix
Encyclopedia
The transfer matrix is a formulation in terms of a block-Toeplitz matrix of the two-scale equation, which characterizes refinable functions. Refinable functions play an important role in wavelet
theory and finite element theory.
For the mask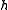 , which is a vector with component indexes from
, which is a vector with component indexes from  to
to 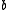 ,
,
the transfer matrix of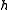 , we call it
, we call it 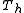 here, is defined as
here, is defined as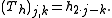
More verbosely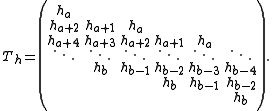
The effect of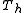 can be expressed in terms of the downsampling
can be expressed in terms of the downsampling
operator "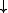 ":
":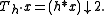
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
theory and finite element theory.
For the mask
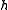 , which is a vector with component indexes from
, which is a vector with component indexes from  to
to 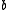 ,
,the transfer matrix of
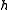 , we call it
, we call it 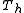 here, is defined as
here, is defined as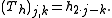
More verbosely
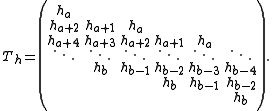
The effect of
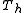 can be expressed in terms of the downsampling
can be expressed in terms of the downsamplingDownsampling
In signal processing, downsampling is the process of reducing the sampling rate of a signal. This is usually done to reduce the data rate or the size of the data....
operator "
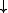 ":
":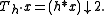
Properties
-
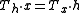 .
. - If you drop the first and the last column and move the odd indexed columns to the left and the even indexed columns to the right, then you obtain a transposed Sylvester matrixSylvester matrixIn mathematics, a Sylvester matrix is a matrix associated to two polynomials that provides information about those polynomials. It is named for James Joseph Sylvester.-Definition:...
. - The determinant of a transfer matrix is essentially a resultant.
- More precisely:
- Let
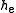 be the even indexed coefficients of
be the even indexed coefficients of 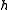 (
(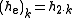 ) and let
) and let 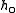 be the odd indexed coefficients of
be the odd indexed coefficients of 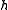 (
(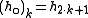 ).
). - Then
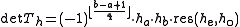 , where
, where 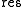 is the resultant.
is the resultant. - This connection allows for fast computation using the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
.- For the traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the transfer matrix of convolvedConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
masks holds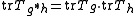
- For the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the transfer matrix of convolved mask holds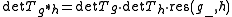
- For the trace
- where
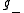 denotes the mask with alternating signs, i.e.
denotes the mask with alternating signs, i.e. 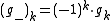 .
.
- If
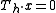 , then
, then 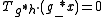 .
.
- If
- This is a concretion of the determinant property above. From the determinant property one knows that
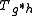 is singular whenever
is singular whenever 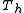 is singular. This property also tells, how vectors from the null spaceNull spaceIn linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
is singular. This property also tells, how vectors from the null spaceNull spaceIn linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of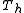 can be converted to null space vectors of
can be converted to null space vectors of 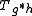 .
.
- If
 is an eigenvector of
is an eigenvector of 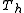 with respect to the eigenvalue
with respect to the eigenvalue 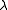 , i.e.
, i.e.
- If
-
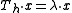 ,
, - then
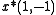 is an eigenvector of
is an eigenvector of 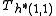 with respect to the same eigenvalue, i.e.
with respect to the same eigenvalue, i.e. -
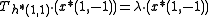 .
.
- Let
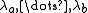 be the eigenvalues of
be the eigenvalues of 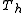 , which implies
, which implies 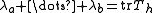 and more generally
and more generally 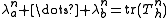 . This sum is useful for estimating the spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
. This sum is useful for estimating the spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of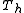 . There is an alternative possibility for computing the sum of eigenvalue powers, which is faster for small
. There is an alternative possibility for computing the sum of eigenvalue powers, which is faster for small  .
.
- Let
- Let
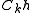 be the periodization of
be the periodization of 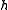 with respect to period
with respect to period 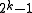 . That is
. That is 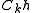 is a circular filter, which means that the component indexes are residue classes with respect to the modulus
is a circular filter, which means that the component indexes are residue classes with respect to the modulus 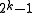 . Then with the upsamplingUpsamplingUpsampling is the process of increasing the sampling rate of a signal. For instance, upsampling raster images such as photographs means increasing the resolution of the image....
. Then with the upsamplingUpsamplingUpsampling is the process of increasing the sampling rate of a signal. For instance, upsampling raster images such as photographs means increasing the resolution of the image....
operator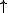 it holds
it holds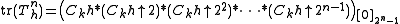
- Actually not
 convolutions are necessary, but only
convolutions are necessary, but only 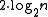 ones, when applying the strategy of efficient computation of powers. Even more the approach can be further sped up using the Fast Fourier transformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
ones, when applying the strategy of efficient computation of powers. Even more the approach can be further sped up using the Fast Fourier transformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
.- From the previous statement we can derive an estimate of the spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of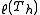 . It holds
. It holds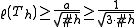
- From the previous statement we can derive an estimate of the spectral radius
- where
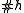 is the size of the filter and if all eigenvalues are real, it is also true that
is the size of the filter and if all eigenvalues are real, it is also true that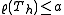 ,
, - where
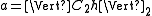 .
.

