Theory of conjoint measurement
Encyclopedia
The theory of conjoint measurement (also known as conjoint measurement or additive conjoint measurement) is a general, formal theory of continuous quantity
. It was independently discovered by the French economist Gerard Debreu
(1960) and by the American mathematical psychologist R. Duncan Luce
and statistician John Tukey
(Luce & Tukey, 1964).
The theory concerns the situation where at least two natural attributes, A and X, non-interactively relate to a third attribute, P. It is not required that A, X or P be already known to be quantities. Via specific relations between the levels of P, it can be established that P, A and X are continuous quantities. Hence the theory of conjoint measurement can be used to quantify attributes in empirical circumstances where it is not possible to combine the levels of the attributes using a side-by-side operation or concatenation
. The quantification of psychological attributes such as attitudes, cognitive abilities and utility is therefore logically plausible. This means that the scientific measurement of psychological attributes is possible. That is, like physical quantities, a magnitude of a psychological quantity may possibly be expressed as the product of a real number
and a unit magnitude.
Application of the theory of conjoint measurement in psychology, however, has been limited. It has been argued that this is due to the high level of formal mathematics involved (e.g., Cliff, 1992) and that the theory cannot account for the "noisy" data typically discovered in psychological research (e.g., Perline, Wright & Wainer, 1979). It has been argued that the Rasch model
is a stochastic variant of the theory of conjoint measurement (e.g., Brogden, 1977; Embretson & Reise, 2000; Fischer, 1995; Keats, 1967; Kline, 1998; Scheiblechner, 1999), however, this has been disputed (e.g., Karabatsos, 2001; Kyngdon, 2008). Order restricted methods for conducting probabilistic tests of the cancellation axioms of conjoint measurement have been developed in the past decade (e.g., Karabatsos, 2001; Davis-Stober, 2009).
The theory of conjoint measurement is not to be confused with conjoint analysis, which is a statistical research methodology employed in marketing
. Conjoint analysis does not at all concern continuous quantity or scientific measurement.
established the Ferguson Committee to investigate the possibility of psychological attributes being measured scientifically. The British physicist and measurement theorist Norman Robert Campbell
was an influential member of the committee.In its Final Report (Ferguson, et al, 1940), Campbell and the Committee concluded that because psychological attributes were not capable of sustaining concatenation operations, such attributes could not be continuous quantities. Therefore, they could not be measured scientifically. This had important ramifications for psychology, the most significant of these being the creation in 1946 of the operational theory of measurement by Harvard psychologist Stanley Smith Stevens
. Stevens' non-scientific theory of measurement is widely held as definitive in psychology and the behavioural sciences generally (Michell, 1999).
Whilst the German mathematician Otto Hölder
(1901) anticipated features of the theory of conjoint measurement, it was not until the publication of Luce & Tukey's seminal 1964 paper that the theory received its first complete exposition. Luce & Tukey's presentation was algebraic and is therefore considered more general than Debreu's (1960) topological work, the latter being a special case of the former (Luce & Suppes, 2002). In the first article of the inaugural issue of the Journal of Mathematical Psychology, Luce & Tukey (1964) proved that via the theory of conjoint measurement, attributes not capable of concatenation could be quantified. N.R. Campbell and the Ferguson Committee were thus proven wrong. That a given psychological attribute is a continuous quantity is a logically coherent and empirically testable hypothesis.
Appearing in the next issue of the same journal were important papers by Dana Scott
(1964), who proposed a hierarchy of cancellation conditions for the indirect testing of the solvability and Archimedean axioms, and David Krantz (1964) who connected the Luce & Tukey work to that of Hölder (1901).
Work soon focused on extending the theory of conjoint measurement to involve more than just two attributes. Krantz (1968) and Amos Tversky (1967) developed what became known as polynomial conjoint measurement
, with Krantz (1968) providing a schema with which to construct conjoint measurement structures of three or more attributes. Later, the theory of conjoint measurement (in its two variable, polynomial and n-component forms) received a thorough and highly technical treatment with the publication of the first volume of Foundations of Measurement, which Krantz, Luce, Tversky and philosopher Patrick Suppes
cowrote (Krantz, Luce, Suppes & Tversky, 1971).
Shortly after the publication of Krantz, et al., (1971), work focused upon developing an "error theory" for the theory of conjoint measurement. Studies were conducted into the number of conjoint arrays that supported only single cancellation and both single and double cancellation (Arbuckle & Larimer, 1976; McClelland, 1977). Later enumeration studies focused on polynomial conjoint measurement (Karabatsos & Ullrich, 2002; Ullrich & Wilson, 1993). These studies found that it is highly unlikely that the axioms of the theory of conjoint measurement are satisfied at random, provided that more than three levels of at least of one the component attributes has been identified.
Joel Michell (1988) later identified that the "no test" class of tests of the double cancellation axiom was empty. Any instance of double cancellation is thus either an acceptance or a rejection of the axiom. Michell also wrote at this time a non-technical introduction to the theory of conjoint measurement (Michell, 1990) which also contained a schema for deriving higher order cancellation conditions based upon Scott's (1964) work. Using Michell's schema, Ben Richards (Kyngdon & Richards, 2007) discovered that some instances of the triple cancellation axiom are "incoherent" as they contradict the single cancellation axiom. Moreover, he identified many instances of the triple cancellation which are trivially true if double cancellation is supported.
The axioms of the theory of conjoint measurement are not stochastic; and given the ordinal constraints placed on data by the cancellation axioms, order restricted inference methodology must be used (Iverson & Falmagne, 1985). George Karabatsos and his associates (Karabatsos, 2001; Karabatsos & Sheu, 2004) developed a Bayesian Markov Chain Monte Carlo
methodology for psychometric applications. Karabatsos & Ullrich (2002) demonstrated how this framework could be extended to polynomial conjoint structures. Karabatsos (2005) generalised this work with his multinomial Dirichlet framework, which enabled the probabilistic testing of many non-stochastic theories of mathematical psychology
. More recently, Clintin Davis-Stober (2009) developed a frequentist framework for order restricted inference that can also be used to test the cancellation axioms.
Perhaps the most notable (Kyngdon, in press) use of the theory of conjoint measurement was in the prospect theory
proposed by the Israeli - American psychologists Daniel Kahneman
and Amos Tverksy (Kahneman & Tversky, 1979). Prospect theory was a theory of decision making under risk and uncertainty which accounted for choice behaviour such as the Allais Paradox
. David Krantz wrote the formal proof to prospect theory using the theory of conjoint measurement. In 2002, Kahneman received the Nobel Memorial Prize in Economics for prospect theory (Birnbaum, 2008).
and metrology
, the standard definition of measurement is the estimation of the ratio between a magnitude of a continuous quantity and a unit magnitude of the same kind (de Boer, 1994/95; Emerson, 2008). For example, the statement "Peter's hallway is 4m long" expresses a measurement of an hitherto unknown length magnitude (the hallway's length) as the ratio of the unit (the metre in this case) to the length of the hallway. The real number "4" is a real number in the strict mathematical sense of this term.
For some other quantities, it is easier or has been convention to estimate ratios between attribute differences. Consider temperature, for example. In the familiar everyday instances, temperature is measured using instruments calibrated in either the Fahrenheit or Celsius scales. What are really being measured with such instruments are the magnitudes of temperature differences. For example, Anders Celsius
defined the unit of the Celsius scale to be 1/100th of the difference in temperature between the freezing and boiling points of water at sea level. A midday temperature measurement of 20 degrees Celsius is simply the ratio of the Celsius unit to the midday temperature.
Formally expressed, a scientific measurement is:
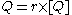
where Q is the magnitude of the quantity, r is a real number and [Q] is a unit magnitude of the same kind.
Temperature is a quantity for which there is an absence of concatenation operations. We cannot pour a volume of water of temperature 40 degrees Celsius into another bucket of water at 20 degrees Celsius and expected to have a volume of water with a temperature of 60 degrees Celsius. Temperature is therefore an intensive quantity.
Psychological attributes, like temperature, are considered to be intensive as no way of concatenating such attributes has been found. But this is not to say that such attributes are not quantifiable. The theory of conjoint measurement provides a theoretical means of doing this.
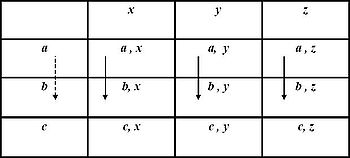The single cancellation axiom is as follows. The relation upon P satisfies single cancellation if and only if for all a and b in A, and x in X, (a, x) > (b, x) is implied for every w in X such that (a, w) > (b, w). Similarly, for all x and y in X and a in A, (a, x) > (a, y) is implied for every d in A such that (d, x) > (d, y). What this means is that if any two levels, a, b, are ordered, then this order holds irrespective of each and every level of X. The same holds for any two levels, x and y of X with respect to each and every level of A.
Single cancellation is so-called because a single common factor of two levels of P cancel out to leave the same ordinal relationship holding on the remaining elements. For example, a cancels out of the inequality (a, x) > (a, y) as it is common to boths sides, leaving x > y. Krantz, et al., (1971) originally called this axiom independence, as the ordinal relation between two levels of an attribute is independent of any and all levels of the other attribute. However, given that the term independence causes confusion with statistical concepts of independence, single cancellation is the preferable term. Figure One is a graphical representation of one instance of single cancellation.
Satisfaction of the single cancellation axiom is necessary, but not sufficient, for the quantification of attributes A and X. It only demonstrates that the levels of A, X and P are ordered. Informally, single cancellation does not sufficiently constrain the order upon the levels of P to quantify A and X. For example, consider the ordered pairs (a, x), (b, x) and (b, y). If single cancellation holds then (a, x) > (b, x) and (b, x) > (b, y). Hence via transitivity (a, x) > (b, y). The relation between these latter two ordered pairs, informally a left-leaning diagonal, is determined by the satisfaction of the single cancellation axiom, as are all the "left leaning diagonal" relations upon P.
Single cancellation does not determine the order of the "right-leaning diagonal" relations upon P. Even though by transitivity and single cancellation it was established that (a, x) > (b, y), the relationship between (a, y) and (b, x) remains undetermined. It could be that either (b, x) > (a, y) or (a, y) > (b, x) and such ambiguity cannot remain unresolved.
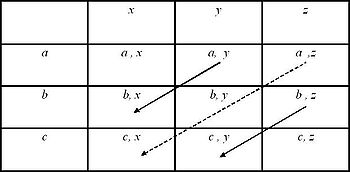
The double cancellation axiom concerns a class of such relations upon P in which the common terms of two antecedent inequalities cancel out to produce a third inequality. Consider the instance of double cancellation graphically represented by Figure Two. The antecedent inequalities of this particular instance of double cancellation are:
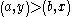
and
.
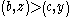Given that:
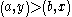
is true if and only if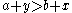
; and
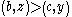
is true if and only if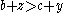
, it follows that:
.
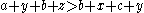Cancelling the common terms results in:
.
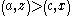Hence double cancellation can only obtain when A and X are quantities.
Double cancellation is satisfied if and only if the consequent inequality does not contradict the antecedent inequalities. For example, if the consequent inequality above was:
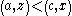, or alternatively,
,
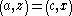then double cancellation would be violated (Michell, 1988) and it could not be concluded that A and X are quantities.
Double cancellation concerns the behaviour of the "right leaning diagonal" relations on P as these are not logically entailed by single cancellation. Michell (2009) discovered that when the levels of A and X approach infinity, then the number of right leaning diagonal relations is half of the number of total relations upon P. Hence if A and X are quantities, half of the number of relations upon P are due to ordinal relations upon A and X and half are due to additive relations upon A and X (Michell, 2009).
The number of instances of double cancellation is contingent upon the number of levels identified for both A and X. If there are n levels of A and m of X, then the number of instances of double cancellation is n! × m!. Therefore, if n = m = 3, then 3! × 3! = 6 × 6 = 36 instances in total of double cancellation. However, all but 6 of these instances are trivially true if single cancellation is true, and if anyone of these 6 instances is true, then all of them are true. One such instance is that shown in Figure Two. Michell (1988) calls this a Luce - Tukey instance of double cancellation.
If single cancellation has been tested upon a set of data first and is established, then only the Luce - Tukey instances of double cancellation need to be tested. For n levels of A and m of X, the number of Luce - Tukey double cancellation instances is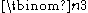
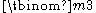. For example, if n = m = 4, then there are 16 such instances. If n = m = 5 then there are 100. The greater the number of levels in both A and X, the less probable it is that the cancellation axioms are satisfied at random (Arbuckle & Larimer, 1976; McClelland, 1977) and the more stringent test of quantity the application of conjoint measurement becomes.
The single and double cancellation axioms by themselves are not sufficient to establish continuous quantity. Other conditions must also be introduced to ensure continuity. These are the solvability and Archimedean conditions.
Solvability means that for any three elements of a, b, x and y, the fourth exists such that the equation a x = b y is solved, hence the name of the condition. Solvability essentially is the requirement that each level P has an element in A and an element in X. Solvability reveals something about the levels of A and X - they are either dense like the real numbers or equally spaced like the integers (Krantz, et al, 1971).
The Archimedean condition is as follows. Let I be a set of consecutive integers, either finite or infinite, positive or negative. The levels of A form a standard sequence if and only if there exists x and y in X where x ≠ y and for all integers i and i + 1 in I:
.
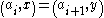What this basically means is that if x is greater than y, for example, there are levels of A which can be found which makes two relevant ordered pairs, the levels of P, equal.
The Archimedean condition argues that there is no infinitely greatest level of P and so hence there is no greatest level of either A or X. This condition is a definition of continuity given by the ancient Greek mathematician Archimedes
whom wrote that “Further, of unequal lines, unequal surfaces, and unequal solids, the greater exceeds the less by such a magnitude as, when added to itself, can be made to exceed any assigned magnitude among those which are comparable with one another ” (On the Sphere and Cylinder, Book I, Assumption 5). Archimedes recognised that for any two magnitudes of a continuous quantity, one being lesser than the other, the lesser could be multiplied by a whole number such that it equalled the greater magnitude. Euclid
stated the Archimedean condition as an axiom in Book V of the Elements
, in which Euclid presented his theory of continuous quantity and measurement.
As they involve infinitistic concepts, the solvability and Archimedean axioms are not amenable to direct testing in any finite empirical situation. But this does not entail that these axioms cannot be empirically tested at all. Scott's (1964) finite set of cancellation conditions can be used to indirectly test these axioms; the extent of such testing being empirically determined. For example, if both A and X possess three levels, the highest order cancellation axiom within Scott’s (1964) hierarchy that indirectly tests solvability and Archimedeaness is double cancellation. With four levels it is triple cancellation (Figure 3). If such tests are satisfied, the construction of standard sequences in differences upon A and X are possible. Hence these attributes may be dense as per the real numbers or equally spaced as per the integers (Krantz, et al., 1971). In other words, A and X are continuous quantities.
Formally, if P, A and X form an additive conjoint structure, then there exist functions from A and X into the real numbers such that for a and b in A and x and y in X:
.
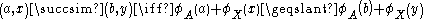If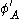
and 
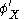are two other real valued functions satisfying the above expression, there exist 
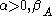and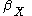 
real valued constants satisfying:
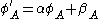and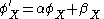 
.
That is,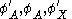
and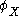 
are measurements of A and X unique up to affine transformation (i.e. each is an interval scale in Stevens’ (1946) parlance). The mathematical proof of this result is given in Krantz, et al. (1971, pp. 261–266).
This means that the levels of A and X are magnitude differences measured relative to some kind of unit difference. Each level of P is a difference between the levels of A and X. However, it is not clear from the literature as to how a unit could be defined within an additive conjoint context. van der Ven (1980) proposed a scaling method for conjoint structures but he also did not discuss the unit.
The theory of conjoint measurement, however, is not restricted to the quantification of differences. If each level of P is a product of a level of A and a level of X, then P is another different quantity whose measurement is expressed as a magnitude of A per unit magnitude of X. For example, A consists of masses and X consists of volumes, then P consists of densities measured as mass per unit of volume. In such cases, it would appear that one level of A and one level of X must be identified as a tentative unit prior to the application of conjoint measurement.
If each level of P is the sum of a level of A and a level of X, then P is the same quantity as A andX. For example, A and X are lengths so hence must be P. All three must therefore be expressed in the same unit. In such cases, it would appear that a level of either A or X must be tentatively identified as the unit. Hence it would seem that application of conjoint measurement requires some prior descriptive theory of the relevant natural system.
Levelt, Riemersma & Bunt (1972) applied the theory to the psychophysics
of binaural loudness. They found the double cancellation axiom was rejected. Gigerenzer & Strube (1983) conducted a similar investigation and replicated Levelt, et al' (1972) findings.
Michell (1990) applied the theory to L.L. Thurstone's (1927) theory of paired comparisons, multidimensional scaling and Coombs' (1964) theory of unidimensional unfolding. He found support of the cancellation axioms only with Coombs' (1964) theory. However, the statistical techniques employed by Michell (1990) in testing Thurstone's theory and multidimensional scaling did not take into consideration the ordinal constraints imposed by the cancellation axioms (van der Linden, 1994).
Johnson (2001), Kyngdon (2006), Michell (1994) and Sherman (1993) tested the cancellation axioms of upon the interstimulus midpoint orders obtained by the use of Coombs' (1964) theory of unidimensional unfolding. Coombs' theory in all three studies was applied to a set of six statements. These authors found that the axioms were satisfied, however, these were applications biased towards a positive result. With six stimuli, the probability of an interstimulus midpoint order satisfying the double cancellation axioms at random is .5874 (Michell, 1994). This is not an unlikely event. Kyngdon & Richards (2007) employed eight statements and found the interstimulus midpoint orders rejected the double cancellation condition.
Perline, Wright and Wainer (1979) applied conjoint measurement to item response data to a convict parole questionnaire and to intelligence test data gathered from Danish troops. They found considerable violation of the cancellation axioms in the parole questionnaire data, but not in the intelligence test data. Moreover, they recorded the supposed "no - test" instances of double cancellation. Interpreting these correctly as instances in support of double cancellation (Michell, 1988), the results of Perline, et al (1979) are better than what they believed.
Stankov & Cregan (1993) applied conjoint measurement to performance on sequence completion tasks. The columns of their conjoint arrays (X) were defined by the demand placed upon working memory capacity through increasing numbers of working memory place keepers in letter series completion tasks. The rows were defined by levels of motivation (A), which consisted in different amount of times available for compelting the test. Their data (P) consisted of completion times and average number of series correct. They found support for the cancellation axioms, however, their study was biased by the small size of the conjoint arrays (3 × 3 is size) and by statistical techniques that did not take into consideration the ordinal restrictions imposed by the cancellation axioms.
Kyngdon (in press) used Karabatsos' (2001) order restricted inference framework to test a conjoint matrix of reading item response proportions (P) where the examinee reading ability comprised the rows of the conjoint array (A) and the difficulty of the reading items formed the columns of the array (X). The levels of reading ability were identified via raw total test score and the levels of reading item difficulty were identified by the Lexile
Framework for Reading (Stenner, Burdick, Sanford & Burdick, 2006). Kyngdon found that satisfaction of the cancellation axioms was obtained only through permutation of the matrix in a manner inconsistent with the putative Lexile measures of item difficulty. Kyngdon also tested simulated ability test response data using polynomial conjoint measurement. The data were generated using Humphry's extended frame of reference Rasch model (Humphry & Andrich, 2008). He found support of distributive, single and double cancellation consistent with a distributive polynomial conjoint structure in three variables (Krantz & Tversky, 1971).
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
. It was independently discovered by the French economist Gerard Debreu
Gerard Debreu
Gérard Debreu was a French economist and mathematician, who also came to have United States citizenship. Best known as a professor of economics at the University of California, Berkeley, where he began work in 1962, he won the 1983 Nobel Memorial Prize in Economics.-Biography:His father was the...
(1960) and by the American mathematical psychologist R. Duncan Luce
R. Duncan Luce
Robert Duncan Luce is the Distinguished Research Professor of Cognitive Science at the University of California, Irvine.Luce received a B.S. in Aeronautical Engineering from the Massachusetts Institute of Technology in 1945, and PhD in Mathematics from the same university in 1950...
and statistician John Tukey
John Tukey
John Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
(Luce & Tukey, 1964).
The theory concerns the situation where at least two natural attributes, A and X, non-interactively relate to a third attribute, P. It is not required that A, X or P be already known to be quantities. Via specific relations between the levels of P, it can be established that P, A and X are continuous quantities. Hence the theory of conjoint measurement can be used to quantify attributes in empirical circumstances where it is not possible to combine the levels of the attributes using a side-by-side operation or concatenation
Concatenation (mathematics)
In mathematics, concatenation is the joining of two numbers by their numerals. That is, the concatenation of 123 and 456 is 123456. Concatenation of numbers a and b is denoted a||b. Relevant subjects in recreational mathematics include Smarandache-Wellin numbers, home primes, and Champernowne's...
. The quantification of psychological attributes such as attitudes, cognitive abilities and utility is therefore logically plausible. This means that the scientific measurement of psychological attributes is possible. That is, like physical quantities, a magnitude of a psychological quantity may possibly be expressed as the product of a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and a unit magnitude.
Application of the theory of conjoint measurement in psychology, however, has been limited. It has been argued that this is due to the high level of formal mathematics involved (e.g., Cliff, 1992) and that the theory cannot account for the "noisy" data typically discovered in psychological research (e.g., Perline, Wright & Wainer, 1979). It has been argued that the Rasch model
Rasch model
Rasch models are used for analysing data from assessments to measure variables such as abilities, attitudes, and personality traits. For example, they may be used to estimate a student's reading ability from answers to questions on a reading assessment, or the extremity of a person's attitude to...
is a stochastic variant of the theory of conjoint measurement (e.g., Brogden, 1977; Embretson & Reise, 2000; Fischer, 1995; Keats, 1967; Kline, 1998; Scheiblechner, 1999), however, this has been disputed (e.g., Karabatsos, 2001; Kyngdon, 2008). Order restricted methods for conducting probabilistic tests of the cancellation axioms of conjoint measurement have been developed in the past decade (e.g., Karabatsos, 2001; Davis-Stober, 2009).
The theory of conjoint measurement is not to be confused with conjoint analysis, which is a statistical research methodology employed in marketing
Marketing
Marketing is the process used to determine what products or services may be of interest to customers, and the strategy to use in sales, communications and business development. It generates the strategy that underlies sales techniques, business communication, and business developments...
. Conjoint analysis does not at all concern continuous quantity or scientific measurement.
Historical overview
In the 1930s, the British Association for the Advancement of ScienceBritish Association for the Advancement of Science
frame|right|"The BA" logoThe British Association for the Advancement of Science or the British Science Association, formerly known as the BA, is a learned society with the object of promoting science, directing general attention to scientific matters, and facilitating interaction between...
established the Ferguson Committee to investigate the possibility of psychological attributes being measured scientifically. The British physicist and measurement theorist Norman Robert Campbell
Norman Robert Campbell
Norman Robert Campbell was an English physicist and philosopher of science. He was educated at Eton and at Trinity College, Cambridge, and became a fellow at Trinity in 1902. He was also a research assistant at the Cavendish Laboratory under the direction of J. J. Thomson...
was an influential member of the committee.In its Final Report (Ferguson, et al, 1940), Campbell and the Committee concluded that because psychological attributes were not capable of sustaining concatenation operations, such attributes could not be continuous quantities. Therefore, they could not be measured scientifically. This had important ramifications for psychology, the most significant of these being the creation in 1946 of the operational theory of measurement by Harvard psychologist Stanley Smith Stevens
Stanley Smith Stevens
Stanley Smith Stevens was an American psychologist who founded Harvard's Psycho-Acoustic Laboratory and is credited with the introduction of Stevens' power law. Stevens authored a milestone textbook, the 1400+ page "Handbook of Experimental Psychology" . He was also one of the founding organizers...
. Stevens' non-scientific theory of measurement is widely held as definitive in psychology and the behavioural sciences generally (Michell, 1999).
Whilst the German mathematician Otto Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
(1901) anticipated features of the theory of conjoint measurement, it was not until the publication of Luce & Tukey's seminal 1964 paper that the theory received its first complete exposition. Luce & Tukey's presentation was algebraic and is therefore considered more general than Debreu's (1960) topological work, the latter being a special case of the former (Luce & Suppes, 2002). In the first article of the inaugural issue of the Journal of Mathematical Psychology, Luce & Tukey (1964) proved that via the theory of conjoint measurement, attributes not capable of concatenation could be quantified. N.R. Campbell and the Ferguson Committee were thus proven wrong. That a given psychological attribute is a continuous quantity is a logically coherent and empirically testable hypothesis.
Appearing in the next issue of the same journal were important papers by Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
(1964), who proposed a hierarchy of cancellation conditions for the indirect testing of the solvability and Archimedean axioms, and David Krantz (1964) who connected the Luce & Tukey work to that of Hölder (1901).
Work soon focused on extending the theory of conjoint measurement to involve more than just two attributes. Krantz (1968) and Amos Tversky (1967) developed what became known as polynomial conjoint measurement
Polynomial conjoint measurement
Polynomial conjoint measurement is an extension of the theory of conjoint measurement to three or more attributes. It was initially developed by the mathematical psychologists David Krantz and Amos Tversky...
, with Krantz (1968) providing a schema with which to construct conjoint measurement structures of three or more attributes. Later, the theory of conjoint measurement (in its two variable, polynomial and n-component forms) received a thorough and highly technical treatment with the publication of the first volume of Foundations of Measurement, which Krantz, Luce, Tversky and philosopher Patrick Suppes
Patrick Suppes
Patrick Colonel Suppes is an American philosopher who has made significant contributions to philosophy of science, the theory of measurement, the foundations of quantum mechanics, decision theory, psychology, and educational technology...
cowrote (Krantz, Luce, Suppes & Tversky, 1971).
Shortly after the publication of Krantz, et al., (1971), work focused upon developing an "error theory" for the theory of conjoint measurement. Studies were conducted into the number of conjoint arrays that supported only single cancellation and both single and double cancellation (Arbuckle & Larimer, 1976; McClelland, 1977). Later enumeration studies focused on polynomial conjoint measurement (Karabatsos & Ullrich, 2002; Ullrich & Wilson, 1993). These studies found that it is highly unlikely that the axioms of the theory of conjoint measurement are satisfied at random, provided that more than three levels of at least of one the component attributes has been identified.
Joel Michell (1988) later identified that the "no test" class of tests of the double cancellation axiom was empty. Any instance of double cancellation is thus either an acceptance or a rejection of the axiom. Michell also wrote at this time a non-technical introduction to the theory of conjoint measurement (Michell, 1990) which also contained a schema for deriving higher order cancellation conditions based upon Scott's (1964) work. Using Michell's schema, Ben Richards (Kyngdon & Richards, 2007) discovered that some instances of the triple cancellation axiom are "incoherent" as they contradict the single cancellation axiom. Moreover, he identified many instances of the triple cancellation which are trivially true if double cancellation is supported.
The axioms of the theory of conjoint measurement are not stochastic; and given the ordinal constraints placed on data by the cancellation axioms, order restricted inference methodology must be used (Iverson & Falmagne, 1985). George Karabatsos and his associates (Karabatsos, 2001; Karabatsos & Sheu, 2004) developed a Bayesian Markov Chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
methodology for psychometric applications. Karabatsos & Ullrich (2002) demonstrated how this framework could be extended to polynomial conjoint structures. Karabatsos (2005) generalised this work with his multinomial Dirichlet framework, which enabled the probabilistic testing of many non-stochastic theories of mathematical psychology
Mathematical psychology
Mathematical psychology is an approach to psychological research that is based on mathematical modeling of perceptual, cognitive and motor processes, and on the establishment of law-like rules that relate quantifiable stimulus characteristics with quantifiable behavior...
. More recently, Clintin Davis-Stober (2009) developed a frequentist framework for order restricted inference that can also be used to test the cancellation axioms.
Perhaps the most notable (Kyngdon, in press) use of the theory of conjoint measurement was in the prospect theory
Prospect theory
Prospect theory is a theory that describes decisions between alternatives that involve risk i.e. where the probabilities of outcomes are known. The model is descriptive: it tries to model real-life choices, rather than optimal decisions.-Model:...
proposed by the Israeli - American psychologists Daniel Kahneman
Daniel Kahneman
Daniel Kahneman is an Israeli-American psychologist and Nobel laureate. He is notable for his work on the psychology of judgment and decision-making, behavioral economics and hedonic psychology....
and Amos Tverksy (Kahneman & Tversky, 1979). Prospect theory was a theory of decision making under risk and uncertainty which accounted for choice behaviour such as the Allais Paradox
Allais paradox
The Allais paradox is a choice problem designed by Maurice Allais to show an inconsistency of actual observed choices with the predictions of expected utility theory.-Statement of the Problem:...
. David Krantz wrote the formal proof to prospect theory using the theory of conjoint measurement. In 2002, Kahneman received the Nobel Memorial Prize in Economics for prospect theory (Birnbaum, 2008).
The classical / standard definition of measurement
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and metrology
Metrology
Metrology is the science of measurement. Metrology includes all theoretical and practical aspects of measurement. The word comes from Greek μέτρον , "measure" + "λόγος" , amongst others meaning "speech, oration, discourse, quote, study, calculation, reason"...
, the standard definition of measurement is the estimation of the ratio between a magnitude of a continuous quantity and a unit magnitude of the same kind (de Boer, 1994/95; Emerson, 2008). For example, the statement "Peter's hallway is 4m long" expresses a measurement of an hitherto unknown length magnitude (the hallway's length) as the ratio of the unit (the metre in this case) to the length of the hallway. The real number "4" is a real number in the strict mathematical sense of this term.
For some other quantities, it is easier or has been convention to estimate ratios between attribute differences. Consider temperature, for example. In the familiar everyday instances, temperature is measured using instruments calibrated in either the Fahrenheit or Celsius scales. What are really being measured with such instruments are the magnitudes of temperature differences. For example, Anders Celsius
Anders Celsius
Anders Celsius was a Swedish astronomer. He was professor of astronomy at Uppsala University from 1730 to 1744, but traveled from 1732 to 1735 visiting notable observatories in Germany, Italy and France. He founded the Uppsala Astronomical Observatory in 1741, and in 1742 he proposed the Celsius...
defined the unit of the Celsius scale to be 1/100th of the difference in temperature between the freezing and boiling points of water at sea level. A midday temperature measurement of 20 degrees Celsius is simply the ratio of the Celsius unit to the midday temperature.
Formally expressed, a scientific measurement is:
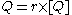
where Q is the magnitude of the quantity, r is a real number and [Q] is a unit magnitude of the same kind.
Extensive and intensive quantity
Length is a quantity for which natural concatenation operations exist. That is, we can combine in a side by side fashion lengths of rigid steel rods, for example, such that the additive relations between lengths is readily observed. If we have four 1m lengths of such rods, we can place them end to end to produce a length of 4m. Quantities capable of concatenation are known as extensive quantities and include mass, time, electrical resistance and plane angle. These are known as base quantities in physics and metrology.Temperature is a quantity for which there is an absence of concatenation operations. We cannot pour a volume of water of temperature 40 degrees Celsius into another bucket of water at 20 degrees Celsius and expected to have a volume of water with a temperature of 60 degrees Celsius. Temperature is therefore an intensive quantity.
Psychological attributes, like temperature, are considered to be intensive as no way of concatenating such attributes has been found. But this is not to say that such attributes are not quantifiable. The theory of conjoint measurement provides a theoretical means of doing this.
Theory
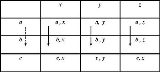
Consider two natural attributes A, and X. It is not known that either A or X is a continuous quantity, or that both of them are. Let a, b, and c represent three independent, identifiable levels of A; and let x, y and z represent three independent, identifiable levels of X. A third attribute, P, consists of the nine ordered pairs of levels of A and X. That is, (a, x), (b, y),..., (c, z) (see Figure 1). The quantification of A, X and P depends upon the behaviour of the relation holding upon the levels of P. These are relations are presented as axioms in the theory of conjoint measurement.Single cancellation or independence axiom
Single cancellation is so-called because a single common factor of two levels of P cancel out to leave the same ordinal relationship holding on the remaining elements. For example, a cancels out of the inequality (a, x) > (a, y) as it is common to boths sides, leaving x > y. Krantz, et al., (1971) originally called this axiom independence, as the ordinal relation between two levels of an attribute is independent of any and all levels of the other attribute. However, given that the term independence causes confusion with statistical concepts of independence, single cancellation is the preferable term. Figure One is a graphical representation of one instance of single cancellation.
Satisfaction of the single cancellation axiom is necessary, but not sufficient, for the quantification of attributes A and X. It only demonstrates that the levels of A, X and P are ordered. Informally, single cancellation does not sufficiently constrain the order upon the levels of P to quantify A and X. For example, consider the ordered pairs (a, x), (b, x) and (b, y). If single cancellation holds then (a, x) > (b, x) and (b, x) > (b, y). Hence via transitivity (a, x) > (b, y). The relation between these latter two ordered pairs, informally a left-leaning diagonal, is determined by the satisfaction of the single cancellation axiom, as are all the "left leaning diagonal" relations upon P.
Double cancellation axiom
The double cancellation axiom concerns a class of such relations upon P in which the common terms of two antecedent inequalities cancel out to produce a third inequality. Consider the instance of double cancellation graphically represented by Figure Two. The antecedent inequalities of this particular instance of double cancellation are:
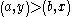
and
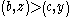.Given that:
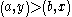
is true if and only if
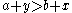; and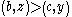is true if and only if
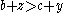, it follows that: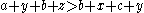.Cancelling the common terms results in:
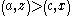.Hence double cancellation can only obtain when A and X are quantities.
Double cancellation is satisfied if and only if the consequent inequality does not contradict the antecedent inequalities. For example, if the consequent inequality above was:
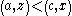, or alternatively,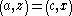,then double cancellation would be violated (Michell, 1988) and it could not be concluded that A and X are quantities.
Double cancellation concerns the behaviour of the "right leaning diagonal" relations on P as these are not logically entailed by single cancellation. Michell (2009) discovered that when the levels of A and X approach infinity, then the number of right leaning diagonal relations is half of the number of total relations upon P. Hence if A and X are quantities, half of the number of relations upon P are due to ordinal relations upon A and X and half are due to additive relations upon A and X (Michell, 2009).
The number of instances of double cancellation is contingent upon the number of levels identified for both A and X. If there are n levels of A and m of X, then the number of instances of double cancellation is n! × m!. Therefore, if n = m = 3, then 3! × 3! = 6 × 6 = 36 instances in total of double cancellation. However, all but 6 of these instances are trivially true if single cancellation is true, and if anyone of these 6 instances is true, then all of them are true. One such instance is that shown in Figure Two. Michell (1988) calls this a Luce - Tukey instance of double cancellation.
If single cancellation has been tested upon a set of data first and is established, then only the Luce - Tukey instances of double cancellation need to be tested. For n levels of A and m of X, the number of Luce - Tukey double cancellation instances is
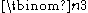
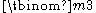. For example, if n = m = 4, then there are 16 such instances. If n = m = 5 then there are 100. The greater the number of levels in both A and X, the less probable it is that the cancellation axioms are satisfied at random (Arbuckle & Larimer, 1976; McClelland, 1977) and the more stringent test of quantity the application of conjoint measurement becomes.Solvability and Archimedean axioms
Solvability means that for any three elements of a, b, x and y, the fourth exists such that the equation a x = b y is solved, hence the name of the condition. Solvability essentially is the requirement that each level P has an element in A and an element in X. Solvability reveals something about the levels of A and X - they are either dense like the real numbers or equally spaced like the integers (Krantz, et al, 1971).
The Archimedean condition is as follows. Let I be a set of consecutive integers, either finite or infinite, positive or negative. The levels of A form a standard sequence if and only if there exists x and y in X where x ≠ y and for all integers i and i + 1 in I:
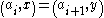.What this basically means is that if x is greater than y, for example, there are levels of A which can be found which makes two relevant ordered pairs, the levels of P, equal.
The Archimedean condition argues that there is no infinitely greatest level of P and so hence there is no greatest level of either A or X. This condition is a definition of continuity given by the ancient Greek mathematician Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
whom wrote that “Further, of unequal lines, unequal surfaces, and unequal solids, the greater exceeds the less by such a magnitude as, when added to itself, can be made to exceed any assigned magnitude among those which are comparable with one another ” (On the Sphere and Cylinder, Book I, Assumption 5). Archimedes recognised that for any two magnitudes of a continuous quantity, one being lesser than the other, the lesser could be multiplied by a whole number such that it equalled the greater magnitude. Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
stated the Archimedean condition as an axiom in Book V of the Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, in which Euclid presented his theory of continuous quantity and measurement.
As they involve infinitistic concepts, the solvability and Archimedean axioms are not amenable to direct testing in any finite empirical situation. But this does not entail that these axioms cannot be empirically tested at all. Scott's (1964) finite set of cancellation conditions can be used to indirectly test these axioms; the extent of such testing being empirically determined. For example, if both A and X possess three levels, the highest order cancellation axiom within Scott’s (1964) hierarchy that indirectly tests solvability and Archimedeaness is double cancellation. With four levels it is triple cancellation (Figure 3). If such tests are satisfied, the construction of standard sequences in differences upon A and X are possible. Hence these attributes may be dense as per the real numbers or equally spaced as per the integers (Krantz, et al., 1971). In other words, A and X are continuous quantities.
Relation to the scientific definition of measurement
Satisfaction of the conditions of conjoint measurement means that measurements of the levels of A and X can be expressed as either ratios between magnitudes or ratios between magnitude differences. It is most commonly interpreted as the latter, given that most behavioural scientists consider that their tests and surveys "measure" attributes on so-called "interval scales" (Kline, 1998). That is, they believe tests do not identify absolute zero levels of psychological attributes.Formally, if P, A and X form an additive conjoint structure, then there exist functions from A and X into the real numbers such that for a and b in A and x and y in X:
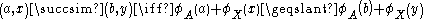.If
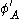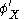and are two other real valued functions satisfying the above expression, there exist 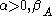and 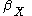real valued constants satisfying: 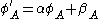and 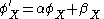.That is,
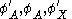and 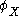are measurements of A and X unique up to affine transformation (i.e. each is an interval scale in Stevens’ (1946) parlance). The mathematical proof of this result is given in Krantz, et al. (1971, pp. 261–266).This means that the levels of A and X are magnitude differences measured relative to some kind of unit difference. Each level of P is a difference between the levels of A and X. However, it is not clear from the literature as to how a unit could be defined within an additive conjoint context. van der Ven (1980) proposed a scaling method for conjoint structures but he also did not discuss the unit.
The theory of conjoint measurement, however, is not restricted to the quantification of differences. If each level of P is a product of a level of A and a level of X, then P is another different quantity whose measurement is expressed as a magnitude of A per unit magnitude of X. For example, A consists of masses and X consists of volumes, then P consists of densities measured as mass per unit of volume. In such cases, it would appear that one level of A and one level of X must be identified as a tentative unit prior to the application of conjoint measurement.
If each level of P is the sum of a level of A and a level of X, then P is the same quantity as A andX. For example, A and X are lengths so hence must be P. All three must therefore be expressed in the same unit. In such cases, it would appear that a level of either A or X must be tentatively identified as the unit. Hence it would seem that application of conjoint measurement requires some prior descriptive theory of the relevant natural system.
Applications of Conjoint Measurement
Empirical applications of the theory of conjoint measurement have been sparse (Cliff, 1992; Michell, 2009).Levelt, Riemersma & Bunt (1972) applied the theory to the psychophysics
Psychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they effect. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, more completely, as "the analysis of perceptual...
of binaural loudness. They found the double cancellation axiom was rejected. Gigerenzer & Strube (1983) conducted a similar investigation and replicated Levelt, et al' (1972) findings.
Michell (1990) applied the theory to L.L. Thurstone's (1927) theory of paired comparisons, multidimensional scaling and Coombs' (1964) theory of unidimensional unfolding. He found support of the cancellation axioms only with Coombs' (1964) theory. However, the statistical techniques employed by Michell (1990) in testing Thurstone's theory and multidimensional scaling did not take into consideration the ordinal constraints imposed by the cancellation axioms (van der Linden, 1994).
Johnson (2001), Kyngdon (2006), Michell (1994) and Sherman (1993) tested the cancellation axioms of upon the interstimulus midpoint orders obtained by the use of Coombs' (1964) theory of unidimensional unfolding. Coombs' theory in all three studies was applied to a set of six statements. These authors found that the axioms were satisfied, however, these were applications biased towards a positive result. With six stimuli, the probability of an interstimulus midpoint order satisfying the double cancellation axioms at random is .5874 (Michell, 1994). This is not an unlikely event. Kyngdon & Richards (2007) employed eight statements and found the interstimulus midpoint orders rejected the double cancellation condition.
Perline, Wright and Wainer (1979) applied conjoint measurement to item response data to a convict parole questionnaire and to intelligence test data gathered from Danish troops. They found considerable violation of the cancellation axioms in the parole questionnaire data, but not in the intelligence test data. Moreover, they recorded the supposed "no - test" instances of double cancellation. Interpreting these correctly as instances in support of double cancellation (Michell, 1988), the results of Perline, et al (1979) are better than what they believed.
Stankov & Cregan (1993) applied conjoint measurement to performance on sequence completion tasks. The columns of their conjoint arrays (X) were defined by the demand placed upon working memory capacity through increasing numbers of working memory place keepers in letter series completion tasks. The rows were defined by levels of motivation (A), which consisted in different amount of times available for compelting the test. Their data (P) consisted of completion times and average number of series correct. They found support for the cancellation axioms, however, their study was biased by the small size of the conjoint arrays (3 × 3 is size) and by statistical techniques that did not take into consideration the ordinal restrictions imposed by the cancellation axioms.
Kyngdon (in press) used Karabatsos' (2001) order restricted inference framework to test a conjoint matrix of reading item response proportions (P) where the examinee reading ability comprised the rows of the conjoint array (A) and the difficulty of the reading items formed the columns of the array (X). The levels of reading ability were identified via raw total test score and the levels of reading item difficulty were identified by the Lexile
Lexile
The Lexile Framework for Reading is an educational tool that uses a measure called a Lexile to match readers of all ages with books, articles and other leveled reading resources....
Framework for Reading (Stenner, Burdick, Sanford & Burdick, 2006). Kyngdon found that satisfaction of the cancellation axioms was obtained only through permutation of the matrix in a manner inconsistent with the putative Lexile measures of item difficulty. Kyngdon also tested simulated ability test response data using polynomial conjoint measurement. The data were generated using Humphry's extended frame of reference Rasch model (Humphry & Andrich, 2008). He found support of distributive, single and double cancellation consistent with a distributive polynomial conjoint structure in three variables (Krantz & Tversky, 1971).