The theorem on friends and strangers is a mathematical theorem in an area of mathematics called Ramsey theory

Ramsey theory

Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...

.

Statement

Suppose a party has six people. Consider any two of them. They might be meeting for the first time—in which case we will call them mutual strangers; or they might have met before—in which case we will call them mutual acquaintances. The theorem says:

In any party of six people either at least three of them are (pairwise) mutual strangers or at least three of them are (pairwise) mutual acquaintances.

Conversion to a graph-theoretic setting

A proof

Mathematical proof

In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...

 of the theorem requires nothing but a three-step logic. It is convenient to phrase the problem in graph-theoretic language.

Suppose a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 has 6 vertices and every pair of vertices is joined by an edge. Such a graph is called a complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

 (because there cannot be any more edges). A complete graph on vertices is denoted by the symbol .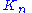

Now take a . It has 15 edges in all. Let the 6 vertices stand for the 6 people in our party. Let the edges be coloured red or blue depending on whether the two people represented by the vertices connected by the edge are mutual strangers or mutual acquaintances, respectively. The theorem now asserts:

No matter how you colour the 15 edges of a 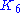with red and blue, you cannot avoid having either a red triangle—that is, a triangle all of whose three sides are red, representing three pairs of mutual strangers—or a blue triangle, representing three pairs of mutual acquaintances. In other words, whatever colours you use, at least one of those two possibilities will occur.

Proof

Choose any one vertex; call it P. There are five edges leaving P. They are each coloured red or blue. The pigeonhole principle says that at least three of them must be of the same colour; for if there are less than three of one colour, say red, then there are at least three that are blue.

Let A, B, C be the other ends of these three edges, all of the same colour, say blue. If any one of AB, BC, CA is blue, then that edge together with the two edges from P to the edge's endpoints forms a blue triangle. If none of AB, BC, CA is blue, then all three edges are red and we have a red triangle, namely, ABC.

Ramsey's paper

The utter simplicity of this argument, which so powerfully produces a very interesting conclusion, is what makes the theorem appealing. In 1930, in a paper entitled 'On a Problem in Formal Logic,' Frank P. Ramsey

Frank P. Ramsey

Frank Plumpton Ramsey was a British mathematician who, in addition to mathematics, made significant and precocious contributions in philosophy and economics before his death at the age of 26...

 proved a very general theorem (now known as Ramsey's theorem

Ramsey's theorem

In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...

) of which this theorem is a simple case. This theorem of Ramsey forms the foundation of the area known as Ramsey theory

Ramsey theory

Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...

 in combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

.

Boundaries to the theorem

The conclusion to the theorem does not hold if we replace the party of six people by a party of less than six. To show this, we give a coloring of K₅ with red and blue that does not contain a triangle with all edges the same color. We draw K₅ as a pentagon surrounding a star. We color the edges of the pentagon red and the edges of the star blue.
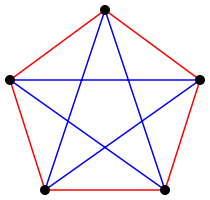
Thus, 6 is the smallest number for which we can claim the conclusion of the theorem. In Ramsey theory, we write this fact as:

External links

• Party Acquaintances at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  (requires Java)