Taylor–Proudman theorem
Encyclopedia
In fluid mechanics
, the Taylor–Proudman theorem (after G. I. Taylor and Joseph Proudman
) states that when a solid body is moved slowly within a fluid that is steadily rotated with a high
, the fluid velocity
will be uniform along any line parallel to the axis of rotation.
must be large compared to the movement of the solid body in order to make the coriolis force large compared to the acceleration terms.
That this is so may be seen by considering the Navier–Stokes equations for steady flow, with zero viscosity and a body force corresponding to the Coriolis force, which are: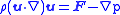
where
is the fluid velocity, 
is the fluid density, and 
the pressure. If we now make the assumption that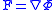 
is scalar potential
and the advective term may be neglected (reasonable if the Rossby number
is much less than unity) and that the flow is incompressible (density is constant) then the equations become:
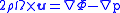
where
the angular velocity
vector. If the curl of this equation is taken, the result is the Taylor–Proudman theorem:
To derive this, one needs the vector identities
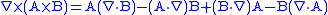
and
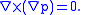
and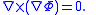
(because curl of gradient is always equal zero)
Note that
is also needed (angular velocity is divergence-free).
The vector form of the Taylor–Proudman theorem is perhaps better understood by expanding the dot product:
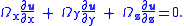
Now choose coordinates in which
and then the equations reduce to
if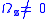
. Note that the implication is that all three components of the velocity vector are uniform along any line parallel to the z-axis.
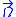axis, often taken to be the 
axis.
The Taylor column is a simplified, experimentally oberved effect of what transpires in the Earth's atmospheres and oceans.
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, the Taylor–Proudman theorem (after G. I. Taylor and Joseph Proudman
Joseph Proudman
Joseph Proudman , CBE, FRS was a distinguished British mathematician and oceanographer of international repute...
) states that when a solid body is moved slowly within a fluid that is steadily rotated with a high
, the fluid velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
will be uniform along any line parallel to the axis of rotation.
must be large compared to the movement of the solid body in order to make the coriolis force large compared to the acceleration terms.That this is so may be seen by considering the Navier–Stokes equations for steady flow, with zero viscosity and a body force corresponding to the Coriolis force, which are:
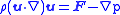
where
is the fluid velocity, is the fluid density, and the pressure. If we now make the assumption that 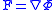is scalar potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
and the advective term may be neglected (reasonable if the Rossby number
Rossby number
The Rossby number, named for Carl-Gustav Arvid Rossby, is a dimensionless number used in describing fluid flow. The Rossby number is the ratio of inertial to Coriolis force, terms v\cdot\nabla v\sim U^2 / L and \Omega\times v\sim U\Omega in the Navier–Stokes equations, respectively...
is much less than unity) and that the flow is incompressible (density is constant) then the equations become:
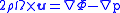
where
the angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector. If the curl of this equation is taken, the result is the Taylor–Proudman theorem:
To derive this, one needs the vector identities
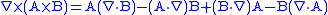
and
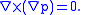
and
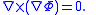
(because curl of gradient is always equal zero)
Note that
is also needed (angular velocity is divergence-free).The vector form of the Taylor–Proudman theorem is perhaps better understood by expanding the dot product:
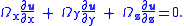
Now choose coordinates in which
and then the equations reduce toif
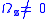. Note that the implication is that all three components of the velocity vector are uniform along any line parallel to the z-axis.Taylor Column
The Taylor column is an imaginary cylinder projected above and below a real cylinder that has been placed parallel to the rotation axis (anywhere in the flow, not necessarily in the center). The flow will curve around the imaginary cylinders just like the real due to the Taylor-Proudman theorem, which states that the flow in a rotating, homogenous, inviscid fluid are 2-dimensional in the plane orthogonal to the rotation axis and thus there is no variation in the flow along the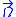axis, often taken to be the axis.The Taylor column is a simplified, experimentally oberved effect of what transpires in the Earth's atmospheres and oceans.