
Tangent half-angle formula
Encyclopedia
In trigonometry
, the tangent half-angle formulas relate the tangent of one half on an angle to trigonometric functions of the entire angle, as follows:
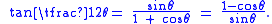
Variations on this theme include the following identities:
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, the tangent half-angle formulas relate the tangent of one half on an angle to trigonometric functions of the entire angle, as follows:
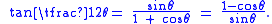
Variations on this theme include the following identities:
-
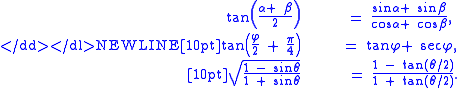
For a restricted domain of θ we have
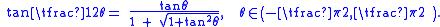
A geometric proof
The Weierstrass substitution
In various applications of trigonometryTrigonometryTrigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, it is useful to rewrite the trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s (such as sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine) in terms of rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s of a new variable t. These identities are known collectively as the tangent half-angle formulae because of the definition of t. These identities can be useful in calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
for converting rational functions in sine and cosine to functions of t in order to find their antiderivativeAntiderivativeIn calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s.
Technically, the existence of the tangent half-angle formulae stems from the fact that the circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is an algebraic curveAlgebraic curveIn algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
0. One then expects that the 'circular functions' should be reducible to rational functions.
Geometrically, the construction goes like this: for any point (cos φ, sin φ) on the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, draw the line passing through it and the point (−1,0). This point crosses the y-axis at some point y = t. One can show using simple geometry that t = tan(φ/2). The equation for the drawn line is y = (1 + x)t. The equation for the intersection of the line and circle is then a quadratic equationQuadratic equationIn mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
involving t. The two solutions to this equation are (−1, 0) and (cos φ, sin φ). This allows us to write the latter as rational functions of t (solutions are given below).
Note also that the parameter t represents the stereographic projectionStereographic projectionThe stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
of the point (cos φ, sin φ) onto the y-axis with the center of projection at (−1,0). Thus, the tangent half-angle formulae give conversions between the stereographic coordinate t on the unit circle and the standard angular coordinate φ.
Then we have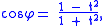
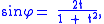

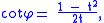
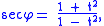

and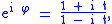
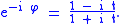
By eliminating phi between the directly above and the initial definition of t, one arrives at the following useful relationship for the arctangent in terms of the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...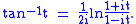
In calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the Weierstrass substitution is used to find antiderivatives of rational functions of sin(φ) and cos(φ). After setting
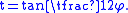
This implies that
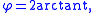
and therefore
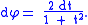
Hyperbolic identities
One can play an entirely analogous game with the hyperbolic functionHyperbolic functionIn mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s. A point on (the right branch of) a hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
is given by (cosh θ, sinh θ). Projecting this onto y-axis from the center (−1, 0) gives the following:
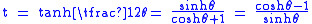
with the identities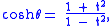
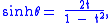
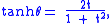
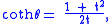

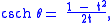
and


The use of this substitution for finding antiderivatives was introduced by Karl WeierstrassKarl WeierstrassKarl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
.
Finding θ in terms of t leads to following relationship between the hyperbolic arctangent and the natural logarithm:
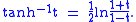
The Gudermannian function
Comparing the hyperbolic identities to the circular ones, one notices that they involve the same functions of t, just permuted. If we identify the parameter t in both cases we arrive at a relationship between the circular functions and the hyperbolic ones. That is, if
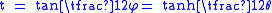
then
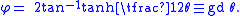
The function gd(θ) is called the Gudermannian function. The Gudermannian function gives a direct relationship between the circular functions and the hyperbolic ones that does not involve complex numbers. The above descriptions of the tangent half-angle formulae (projection the unit circle and standard hyperbola onto the y-axis) give a geometric interpretation of this function.
External links
- Tangent Of Halved Angle at PlanetmathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Tangent Of Halved Angle at Planetmath

