In mathematics, a Tamari lattice, introduced by , is a partially ordered set

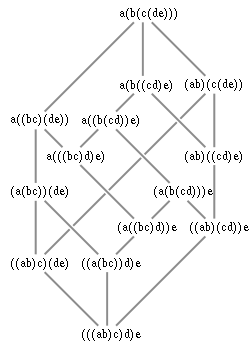
Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

 in which the elements consist of different ways of grouping a sequence of objects into pairs using parentheses; for instance, for a sequence of four objects abcd, the five possible groupings are ((ab)c)d, (ab)(cd), (a(bc))d, a((bc)d), and a(b(cd)). Each grouping describes a different order in which the objects may be combined by a binary operation

Binary operation

In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....

; in the Tamari lattice, one grouping is ordered before another if the second grouping may be obtained from the first by only rightward applications of the associative law

Associativity

In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...

 (xy)z = x(yz). For instance, applying this law with x = a, y = bc, and z = d gives the expansion (a(bc))d = a((bc)d), so in the ordering of the Tamari lattice (a(bc))d ≤ a((bc)d).

In this partial order, any two groupings g₁ and g₂ have a greatest common predecessor, the meet g₁ ∧ g₂, and a least common successor, the join g₁ ∨ g₂. Thus, the Tamari lattice has the structure of a lattice

Lattice (order)

In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...

. The Hasse diagram

Hasse diagram

In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...

 of this lattice is isomorphic

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

 to the vertex-edge incidence graph of an associahedron

Associahedron

In mathematics, an associahedron or Stasheff polytope Kn is a convex polytope in which each vertex corresponds to a way of correctly inserting opening and closing parentheses in a word of n letters and the edges correspond to single application of the associativity rule.Initially Jim Stasheff...

. The number of elements in a Tamari lattice for a sequence of n + 1 objects is the nth Catalan number

Catalan number

In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...

.

The Tamari lattice can also be described in several other equivalent ways:

• It is the poset of sequences of n integers a₁, ..., a_n, ordered coordinatewise, such that i ≤ a_i ≤ n and if i ≤ j ≤ a_i then a_j ≤ a_i .
• It is the poset of binary tree
  Binary tree
  In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
  
  s with n leaves, ordered by tree rotation
  Tree rotation
  A tree rotation is an operation on a binary tree that changes the structure without interfering with the order of the elements. A tree rotation moves one node up in the tree and one node down...
  
   operations.
• It is the poset of ordered forests
  Tree (graph theory)
  In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
  
  , in which one forest is earlier than another in the partial order if, for every j, the jth node in a preorder
  Preorder
  In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
  
   traversal of the first forest has at least as many descendants as the jth node in a preorder traversal of the second forest .
• It is the poset of triangulations of a convex n-gon, ordered by flip operations that substitute one diagonal of the polygon for another.