
Symplectic frame bundle
Encyclopedia
In symplectic geometry, the symplectic frame bundle of a given symplectic manifold
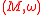 is the canonical principal
is the canonical principal 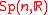 -subbundle
-subbundle
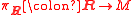 of the tangent frame bundle
of the tangent frame bundle 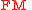 consisting of linear frames which are symplectic with respect to
consisting of linear frames which are symplectic with respect to 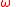 . In other words, an element of the symplectic frame bundle is a linear frame
. In other words, an element of the symplectic frame bundle is a linear frame 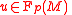 at point
at point 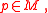 i.e. an ordered basis
i.e. an ordered basis  of tangent vectors at
of tangent vectors at  of the tangent vector space
of the tangent vector space 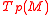 , satisfying
, satisfying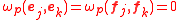 and
and 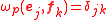
for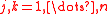 . For
. For  , each fiber
, each fiber 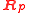 of the principal
of the principal 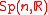 -bundle
-bundle 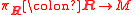 is the set of all symplectic bases of
is the set of all symplectic bases of 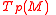 .
.
The symplectic frame bundle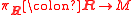 , a subbundle of the tangent frame bundle
, a subbundle of the tangent frame bundle 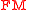 , is an example of reductive G-structure
, is an example of reductive G-structure
on the manifold .
.
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
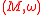 is the canonical principal
is the canonical principal 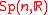 -subbundle
-subbundleSubbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
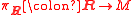 of the tangent frame bundle
of the tangent frame bundle 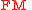 consisting of linear frames which are symplectic with respect to
consisting of linear frames which are symplectic with respect to  . In other words, an element of the symplectic frame bundle is a linear frame
. In other words, an element of the symplectic frame bundle is a linear frame 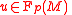 at point
at point 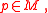 i.e. an ordered basis
i.e. an ordered basis  of tangent vectors at
of tangent vectors at  of the tangent vector space
of the tangent vector space 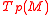 , satisfying
, satisfying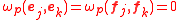 and
and 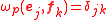
for
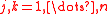 . For
. For  , each fiber
, each fiber 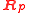 of the principal
of the principal 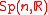 -bundle
-bundle 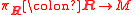 is the set of all symplectic bases of
is the set of all symplectic bases of 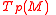 .
.The symplectic frame bundle
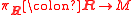 , a subbundle of the tangent frame bundle
, a subbundle of the tangent frame bundle 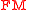 , is an example of reductive G-structure
, is an example of reductive G-structureG-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
on the manifold
 .
.See also
- Metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
- Metaplectic structureMetaplectic structureIn differential geometry, a metaplectic structure is the symplectic analog of spin structure on orientable Riemannian manifolds. A metaplectic structure on a symplectic manifold allows one to define the symplectic spinor bundle, which is the Hilbert space bundle associated to the metaplectic...
- Symplectic structure
- Symplectic geometry
- Symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
- Symplectic spinor bundle
Books
- da Silva, A.C., Lectures on Symplectic Geometry, Springer (2001). ISBN 3-540-42195-5.
- Maurice de Gosson: Symplectic Geometry and Quantum Mechanics (2006) Birkhäuser Verlag, Basel ISBN 3-7643-7574-1.

