Surrogate model
Encyclopedia
Most engineering design problems require experiments and/or simulations to evaluate design objective and constraint functions as function of design variables. For example, in order to find the optimal airfoil shape for an aircraft wing, an engineer simulates the air flow around the wing for different shape variables (length, curvature, material, ..). For many real world problems, however, a single simulation can take many minutes, hours, or even days to complete. As a result, routine tasks such as design optimization, design space exploration, sensitivity analysis and what-if analysis become impossible since they require thousands or even millions of simulation evaluations.
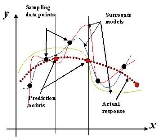
One way of alleviating this burden is by constructing approximation models, known as surrogate models, response surface models
, metamodels or emulators, that mimic the behavior of the simulation model as closely as possible while being computationally cheap(er) to evaluate. Surrogate models are constructed using a data-driven, bottom-up approach. The exact, inner working of the simulation code is not assumed to be known (or even understood), solely the input-output behavior is important. A model is constructed based on modeling the response of the simulator to a limited number of intelligently chosen data points. This approach is also known as behavioral modeling or black-box modeling, though the terminology is not always consistent. When only a single design variable is involved, the process is known as curve fitting
as illustrated in the Figure.
While this article is written around the subject of using surrogate models in lieu of experiments and simulations in engineering design, surrogate modelling may be used in many other areas of science where there are expensive experiments and/or function evaluations.
An important distinction can be made between two different applications of surrogate models: design optimization and design space approximation (also known as emulation).
In surrogate model based optimization an initial surrogate is constructed using some of the available budget of expensive experiments and/or simulations. The remaining experiments/simulations are run for designs which the surrogate model predicts may have promising performance. The process usually takes the form of the following search/update procedure.
Depending on the type of surrogate used and the complexity of the problem, the process may converge on a local or global optimum, or perhaps none at all.
In design space approximation, one is not interested in finding the optimal parameter vector but rather in the global behavior of the system. Here the surrogate is tuned to mimic the underlying model as closely as needed over the complete design space. Such surrogates are a useful, cheap way to gain insight into the global behavior of the system. Optimization can still occur as a post processing step, although with no update procedure (see above) the optimum found cannot be validated.
The scientific challenge of surrogate modeling is the generation of a surrogate that is as accurate as possible, using as few simulation evaluations as possible. The process comprises three major steps which may be interleaved iteratively:
The accuracy of the surrogate depends on the number and location of samples (expensive experiments or simulations) in the design space. Various design of experiments
(DOE) techniques cater to different sources of errors, in particular errors due to noise in the data or errors due to an improper surrogate model.
The most popular surrogate models are polynomial response surfaces, Kriging
, support vector machine
s and artificial neural networks. For most problems, the nature of true function is not known a priori so it is not clear which surrogate model will be most accurate. In addition, there is no consensus on how to obtain the most reliable estimates of the accuracy of a given surrogate.
One way of alleviating this burden is by constructing approximation models, known as surrogate models, response surface models
Response surface methodology
In statistics, response surface methodology explores the relationships between several explanatory variables and one or more response variables. The method was introduced by G. E. P. Box and K. B. Wilson in 1951. The main idea of RSM is to use a sequence of designed experiments to obtain an...
, metamodels or emulators, that mimic the behavior of the simulation model as closely as possible while being computationally cheap(er) to evaluate. Surrogate models are constructed using a data-driven, bottom-up approach. The exact, inner working of the simulation code is not assumed to be known (or even understood), solely the input-output behavior is important. A model is constructed based on modeling the response of the simulator to a limited number of intelligently chosen data points. This approach is also known as behavioral modeling or black-box modeling, though the terminology is not always consistent. When only a single design variable is involved, the process is known as curve fitting
Curve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
as illustrated in the Figure.
While this article is written around the subject of using surrogate models in lieu of experiments and simulations in engineering design, surrogate modelling may be used in many other areas of science where there are expensive experiments and/or function evaluations.
An important distinction can be made between two different applications of surrogate models: design optimization and design space approximation (also known as emulation).
In surrogate model based optimization an initial surrogate is constructed using some of the available budget of expensive experiments and/or simulations. The remaining experiments/simulations are run for designs which the surrogate model predicts may have promising performance. The process usually takes the form of the following search/update procedure.
- 1. Initial sample selection (the experiments and/or simulations to be run)
- 2. Construct surrogate model
- 3. Search surrogate model (the model can be searched extensively, e.g. using a genetic algorithmGenetic algorithmA genetic algorithm is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems...
, as it is cheap to evaluate) - 4. Run and update experiment/simulation at new location(s) found by search and add to sample
- 5. Iterate steps 2 to 4 until out of time or design 'good enough'
Depending on the type of surrogate used and the complexity of the problem, the process may converge on a local or global optimum, or perhaps none at all.
In design space approximation, one is not interested in finding the optimal parameter vector but rather in the global behavior of the system. Here the surrogate is tuned to mimic the underlying model as closely as needed over the complete design space. Such surrogates are a useful, cheap way to gain insight into the global behavior of the system. Optimization can still occur as a post processing step, although with no update procedure (see above) the optimum found cannot be validated.
The scientific challenge of surrogate modeling is the generation of a surrogate that is as accurate as possible, using as few simulation evaluations as possible. The process comprises three major steps which may be interleaved iteratively:
- Sample selection (also known as sequential design, optimal experimental design (OED) or active learning)
- Construction of the surrogate model and optimizing the model parameters (Bias-Variance trade-off)
- Appraisal of the accuracy of the surrogate.
The accuracy of the surrogate depends on the number and location of samples (expensive experiments or simulations) in the design space. Various design of experiments
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
(DOE) techniques cater to different sources of errors, in particular errors due to noise in the data or errors due to an improper surrogate model.
The most popular surrogate models are polynomial response surfaces, Kriging
Kriging
Kriging is a group of geostatistical techniques to interpolate the value of a random field at an unobserved location from observations of its value at nearby locations....
, support vector machine
Support vector machine
A support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
s and artificial neural networks. For most problems, the nature of true function is not known a priori so it is not clear which surrogate model will be most accurate. In addition, there is no consensus on how to obtain the most reliable estimates of the accuracy of a given surrogate.
Reading
- Queipo, N.V., Haftka, R.T., Shyy, W.Wei ShyyWei Shyy is the Clarence L. "Kelly" Johnson Collegiate Professor and Chairman of the Department of Aerospace Engineering at the University of Michigan in Ann Arbor. He also served as a Distinguished Professor at the University of Florida...
, Goel, T., Vaidyanathan, R., Tucker, P.K. (2005), “Surrogate-based analysis and optimization,” Progress in Aerospace Sciences, 41, 1-28. - D. Gorissen, I. Couckuyt, P. Demeester, T. Dhaene, K. Crombecq, (2010), “A Surrogate Modeling and Adaptive Sampling Toolbox for Computer Based Design," Journal of Machine Learning Research, Vol. 11, pp. 2051−2055, July 2010.
- T-Q. Pham, A. Kamusella, H. Neubert, “Auto-Extraction of Modelica Code from Finite Element Analysis or Measurement Data," 8th International Modelica Conference, 20-22 March 2011 in Dresden.

