Surgery obstruction
Encyclopedia
In mathematics
, specifically in surgery theory
, the surgery obstructions define a map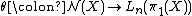
from the normal invariants to the L-group
s which is in the first instance a set-theoretic map (that means not necessarily a homomorphism
) with the following property when
:
A degree-one normal map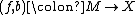
is normally cobordant to a homotopy equivalence if and only if the image 
in 
.
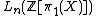Consider a degree-one normal map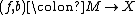
. The idea in deciding the question whether it is normally cobordant to a homotopy equivalence is to try to systematically improve 
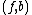so that the map 
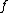becomes 
-connected (that means the homotopy groups 
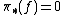for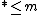 
) for high 
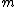. It is a consequence of Poincaré duality
that if we can achieve this for
then the map 
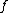already is a homotopy equivalence. The word systematically above refers to the fact that one tries to do surgeries on 
to kill elements of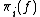 
. In fact it is more convenient to use homology
of the universal covers to observe how connected the map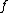
is. More precisely, one works with the surgery kernels 
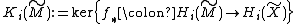which one views as 
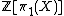-modules. If all these vanish, then the map 
is a homotopy equivalence. As a consequence of Poincaré duality on 
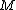and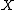 
there is a 
-modules Poincaré duality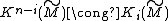 
, so one only has to watch half of them, that means those for which 
.
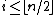Any degree-one normal map can be made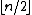
-connected by the process called surgery below the middle dimension. This is the process of killing elements of 
for 
described here
when we have
such that 
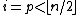. After this is done there are two cases.
1. If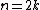
then the only nontrivial homology group is the kernel 
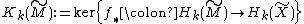. It turns out that the cup-product pairings on 
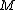and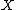 
induce a cup-product pairing on 
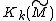. This defines a symmetric bilinear form in case 
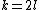and a skew-symmetric bilinear form in case 
. It turns out that these forms can be refined to 
-quadratic forms, where 
. These 
-quadratic forms define elements in the L-groups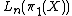 
.
2. If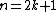
the definition is more complicated. Instead of a quadratic form one obtains from the geometry a quadratic formation, which is a kind of automorphism of quadratic forms. Such a thing defines an element in the odd-dimensional L-group 
.
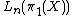If the element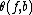
is zero in the L-group surgery can be done on 
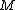to modify 
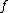to a homotopy equivalence.
Geometrically the reason why this is not always possible is that performing surgery in the middle dimension to kill an element in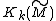
possibly creates an element in 
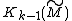whe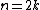n 
or in 
when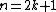 
. So this possibly destroys what has already been achieved. However, if 
is zero, surgeries can be arranged in such a way that this does not happen.
If
there is no obstruction.
If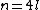
then the surgery obstruction can be calculated as the difference of the signatures of M and X.
If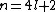
then the surgery obstruction is the Arf-invariant of the associated kernel quadratic form over 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in surgery theory
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
, the surgery obstructions define a map
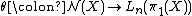from the normal invariants to the L-groupL-group
In mathematics, L-group may refer to the following groups:* The Langlands dual, LG, of a reductive algebraic group G* A group in L-theory, L...
s which is in the first instance a set-theoretic map (that means not necessarily a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
) with the following property when
:A degree-one normal map
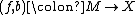is normally cobordant to a homotopy equivalence if and only if the image in 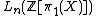.Sketch of the definition
The surgery obstruction of a degree-one normal map has a relatively complicated definition.Consider a degree-one normal map
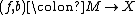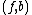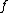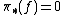. The idea in deciding the question whether it is normally cobordant to a homotopy equivalence is to try to systematically improve so that the map becomes -connected (that means the homotopy groups for 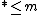) for high 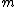. It is a consequence of Poincaré dualityPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
that if we can achieve this for
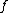then the map already is a homotopy equivalence. The word systematically above refers to the fact that one tries to do surgeries on to kill elements of 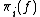. In fact it is more convenient to use homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of the universal covers to observe how connected the map
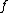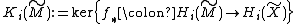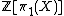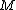is. More precisely, one works with the surgery kernels which one views as -modules. If all these vanish, then the map is a homotopy equivalence. As a consequence of Poincaré duality on and 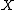there is a -modules Poincaré duality 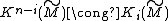, so one only has to watch half of them, that means those for which 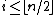.Any degree-one normal map can be made
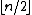-connected by the process called surgery below the middle dimension. This is the process of killing elements of for described hereSurgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
when we have
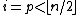such that . After this is done there are two cases.1. If
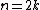then the only nontrivial homology group is the kernel 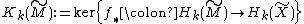. It turns out that the cup-product pairings on 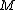and 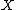induce a cup-product pairing on 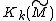. This defines a symmetric bilinear form in case 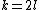and a skew-symmetric bilinear form in case . It turns out that these forms can be refined to -quadratic forms, where . These -quadratic forms define elements in the L-groups 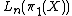.2. If
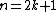the definition is more complicated. Instead of a quadratic form one obtains from the geometry a quadratic formation, which is a kind of automorphism of quadratic forms. Such a thing defines an element in the odd-dimensional L-group 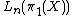.If the element
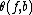is zero in the L-group surgery can be done on 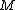to modify 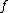to a homotopy equivalence.Geometrically the reason why this is not always possible is that performing surgery in the middle dimension to kill an element in
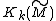possibly creates an element i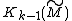n whe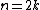n or in when 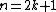. So this possibly destroys what has already been achieved. However, if is zero, surgeries can be arranged in such a way that this does not happen.Example
In the simply connected case the following happens.If
there is no obstruction.If
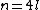then the surgery obstruction can be calculated as the difference of the signatures of M and X.If
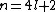then the surgery obstruction is the Arf-invariant of the associated kernel quadratic form over .