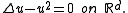Superprocess
Encyclopedia
An 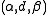 -superprocess,
-superprocess,  , is a stochastic process
, is a stochastic process
on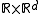 that is usually constructed as a special limit of branching diffusion where the branching mechanism is given by its factorial moment generating function:
that is usually constructed as a special limit of branching diffusion where the branching mechanism is given by its factorial moment generating function: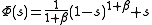
and the spatial motion of individual particles is given by the -symmetric stable process
-symmetric stable process
with infinitesimal generator
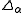 .
.
The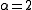 case corresponds to standard Brownian motion
case corresponds to standard Brownian motion
and the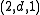 -superprocess is called the Dawson-Watanabe superprocess or super-Brownian motion.
-superprocess is called the Dawson-Watanabe superprocess or super-Brownian motion.
One of the most important properties of superprocesses is that they are intimately connected with certain nonlinear partial differential equations.
The simplest such equation is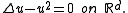
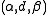 -superprocess,
-superprocess,  , is a stochastic process
, is a stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
on
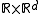 that is usually constructed as a special limit of branching diffusion where the branching mechanism is given by its factorial moment generating function:
that is usually constructed as a special limit of branching diffusion where the branching mechanism is given by its factorial moment generating function: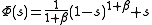
and the spatial motion of individual particles is given by the
 -symmetric stable process
-symmetric stable processLévy process
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
with infinitesimal generator
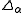 .
.The
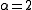 case corresponds to standard Brownian motion
case corresponds to standard Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
and the
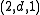 -superprocess is called the Dawson-Watanabe superprocess or super-Brownian motion.
-superprocess is called the Dawson-Watanabe superprocess or super-Brownian motion.One of the most important properties of superprocesses is that they are intimately connected with certain nonlinear partial differential equations.
The simplest such equation is