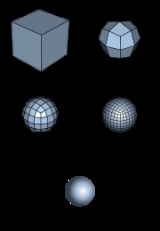
Subdivision surface
Encyclopedia
A subdivision surface, in the field of 3D computer graphics
, is a method of representing a smooth surface
via the specification of a coarser piecewise linear polygon mesh
. The smooth surface can be calculated from the coarse mesh as the limit
of a recursive
process of subdividing each polygonal face
into smaller faces that better approximate the smooth surface.
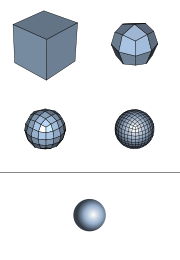
This process produces a denser mesh than the original one, containing more polygonal faces. This resulting mesh can be passed through the same refinement scheme again and so on.
The limit subdivision surface is the surface produced from this process being iteratively applied infinitely many times. In practical use however, this algorithm is only applied a limited number of times. The limit surface can also be calculated directly for most subdivision surfaces using the technique of Jos Stam, which eliminates the need for recursive refinement.
surfaces and curves, where Bézier splines are required to interpolate certain control points, while B-spline
s are not.
There is another division in subdivision surface schemes as well, the type of polygon that they operate on. Some function for quadrilaterals (quads), while others operate on triangles.
A surface designer may also start with a scanned in object or one created from a NURBS surface. The same basic optimization algorithms are used to create a coarse base mesh with the correct topology and then add details at each level so that the object may be edited at different levels. These types of surfaces may be difficult to work with because the base mesh does not have control points in the locations that a human designer would place them. With a scanned object this surface is easier to work with than a raw triangle mesh, but a NURBS object probably had well laid out control points which behave less intuitively after the conversion than before.
3D computer graphics
3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
, is a method of representing a smooth surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
via the specification of a coarser piecewise linear polygon mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...
. The smooth surface can be calculated from the coarse mesh as the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
process of subdividing each polygonal face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
into smaller faces that better approximate the smooth surface.

Overview
The subdivision surfaces are defined recursively. The process starts with a given polygonal mesh. A refinement scheme is then applied to this mesh. This process takes that mesh and subdivides it, creating new vertices and new faces. The positions of the new vertices in the mesh are computed based on the positions of nearby old vertices. In some refinement schemes, the positions of old vertices might also be altered (possibly based on the positions of new vertices).This process produces a denser mesh than the original one, containing more polygonal faces. This resulting mesh can be passed through the same refinement scheme again and so on.
The limit subdivision surface is the surface produced from this process being iteratively applied infinitely many times. In practical use however, this algorithm is only applied a limited number of times. The limit surface can also be calculated directly for most subdivision surfaces using the technique of Jos Stam, which eliminates the need for recursive refinement.
Refinement schemes
Subdivision surface refinement schemes can be broadly classified into two categories: interpolating and approximating. Interpolating schemes are required to match the original position of vertices in the original mesh. Approximating schemes are not; they can and will adjust these positions as needed. In general, approximating schemes have greater smoothness, but editing applications that allow users to set exact surface constraints require an optimization step. This is analogous to splineSpline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
surfaces and curves, where Bézier splines are required to interpolate certain control points, while B-spline
B-spline
In the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
s are not.
There is another division in subdivision surface schemes as well, the type of polygon that they operate on. Some function for quadrilaterals (quads), while others operate on triangles.
Approximating schemes
Approximating means that the limit surfaces approximate the initial meshes and that after subdivision, the newly generated control points are not in the limit surfaces. Examples of approximating subdivision schemes are:- Catmull and Clark (1978) generalized bi-cubic uniform B-spline to produce their subdivision scheme. For arbitrary initial meshes, this scheme generates limit surfaces that are C2 continuous everywhere except at extraordinary vertices where they are C1 continuous (Peters and Reif 1998).
- Doo–Sabin - The second subdivision scheme was developed by Doo and Sabin (1978) who successfully extended Chaikin's corner-cutting method for curves to surfaces. They used the analytical expression of bi-quadratic uniform B-spline surface to generate their subdivision procedure to produce C1 limit surfaces with arbitrary topology for arbitrary initial meshes.
- LoopLoop subdivision surfaceIn computer graphics, Loop subdivision surface is a subdivision scheme developed by Charles Loop in 1987 for triangular meshes.Each triangle is divided into four subtriangles, adding new vertices in the middle of each edge.- External links :...
, Triangles - Loop (1987) proposed his subdivision scheme based on a quartic box-spline of six direction vectors to provide a rule to generate C2 continuous limit surfaces everywhere except at extraordinary vertices where they are C1 continuous. - Mid-Edge subdivision scheme - The mid-edge subdivision scheme was proposed independently by Peters-Reif (1997) and Habib-Warren (1999). The former used the mid-point of each edge to build the new mesh. The latter used a four-directional box spline to build the scheme. This scheme generates C1 continuous limit surfaces on initial meshes with arbitrary topology.
- √3 subdivision scheme - This scheme has been developed by Kobbelt (2000) and offers several interesting features: it handles arbitrary triangular meshes, it is C2 continuous everywhere except at extraordinary vertices where it is C1 continuous and it offers a natural adaptive refinement when required. It exhibits at least two specificities: it is a Dual scheme for triangle meshes and it has a slower refinement rate than primal ones.
Interpolating schemes
After subdivision, the control points of the original mesh and the new generated control points are interpolated on the limit surface. The earliest work was the butterfly scheme by Dyn, Levin and Gregory (1990), who extended the four-point interpolatory subdivision scheme for curves to a subdivision scheme for surface. Zorin, Schröder and Swelden (1996) noticed that the butterfly scheme cannot generate smooth surfaces for irregular triangle meshes and thus modified this scheme. Kobbelt (1996) further generalized the four-point interpolatory subdivision scheme for curves to the tensor product subdivision scheme for surfaces.- Butterfly, Triangles - named after the scheme's shape
- Midedge, Quads
- Kobbelt, Quads - a variational subdivision method that tries to overcome uniform subdivision drawbacks
Editing a subdivision surface
Subdivision surfaces can be naturally edited at different levels of subdivision. Starting with basic shapes you can use binary operators to create the correct topology. Then edit the coarse mesh to create the basic shape, then edit the offsets for the next subdivision step, then repeat this at finer and finer levels. You can always see how your edit effect the limit surface via GPU evaluation of the surface.A surface designer may also start with a scanned in object or one created from a NURBS surface. The same basic optimization algorithms are used to create a coarse base mesh with the correct topology and then add details at each level so that the object may be edited at different levels. These types of surfaces may be difficult to work with because the base mesh does not have control points in the locations that a human designer would place them. With a scanned object this surface is easier to work with than a raw triangle mesh, but a NURBS object probably had well laid out control points which behave less intuitively after the conversion than before.
Key developments
- 1978: Subdivision surfaces were discovered simultaneously by Edwin CatmullEdwin CatmullDr. Edwin Earl Catmull, Ph.D. is a computer scientist and current president of Walt Disney Animation Studios and Pixar Animation Studios. As a computer scientist, Catmull has contributed to many important developments in computer graphics....
and Jim ClarkJames H. ClarkJames H. Clark is an American entrepreneur and computer scientist. He founded several notable Silicon Valley technology companies, including Silicon Graphics, Inc., Netscape Communications Corporation, myCFO and Healtheon...
(see Catmull–Clark subdivision surface). In the same year, Daniel Doo and Malcom Sabin published a paper building on this work (see Doo-Sabin subdivision surfaces.) - 1995: Ulrich Reif solved subdivision surface behaviour near extraordinary vertices.
- 1998: Jos StamJos StamJos Stam is a researcher in the field of computer graphics, focusing on subdivision surfaces, rendering algorithms and the simulation of natural physical phenomena.-Education and career:...
contributed a method for exact evaluation for Catmull–Clark and Loop subdivision surfaces under arbitrary parameter values.
External links
- Resources about Subdvisions
- Geri's Game : Oscar winning animation by PixarPixarPixar Animation Studios, pronounced , is an American computer animation film studio based in Emeryville, California. The studio has earned 26 Academy Awards, seven Golden Globes, and three Grammy Awards, among many other awards and acknowledgments. Its films have made over $6.3 billion worldwide...
completed in 1997 that introduced subdivision surfaces (along with cloth simulation) - Subdivision for Modeling and Animation tutorial, SIGGRAPHSIGGRAPHSIGGRAPH is the name of the annual conference on computer graphics convened by the ACM SIGGRAPH organization. The first SIGGRAPH conference was in 1974. The conference is attended by tens of thousands of computer professionals...
1999 course notes - Subdivision for Modeling and Animation tutorial, SIGGRAPHSIGGRAPHSIGGRAPH is the name of the annual conference on computer graphics convened by the ACM SIGGRAPH organization. The first SIGGRAPH conference was in 1974. The conference is attended by tens of thousands of computer professionals...
2000 course notes - Subdivision of Surface and Volumetric Meshes, software to perform subdivision using the most popular schemes
- Surface Subdivision Methods in CGAL, the Computational Geometry Algorithms Library

