
Strong generating set
Encyclopedia
In abstract algebra
, especially in the area of group theory
, a strong generating set of a permutation group
is a generating set
that clearly exhibits the permutation structure as described by a stabilizer chain. A stabilizer chain is a sequence of subgroup
s, each containing the next and each stabilizing one more point.
Let be a group of permutations
be a group of permutations
of the set Let
Let
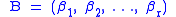
be a sequence of distinct integers,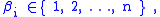 such that the pointwise stabilizer
such that the pointwise stabilizer
of is trivial (i.e., let
is trivial (i.e., let  be a base
be a base
for ). Define
). Define
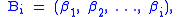
and define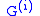 to be the pointwise stabilizer of
to be the pointwise stabilizer of 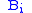 . A strong generating set (SGS) for G relative to the base
. A strong generating set (SGS) for G relative to the base  is a set
is a set
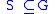
such that
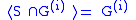
for each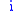 such that
such that 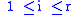 .
.
The base and the SGS are said to be non-redundant if
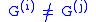
for .
.
A base and strong generating set (BSGS) for a group can be computed using the Schreier–Sims algorithm.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, especially in the area of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a strong generating set of a permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
is a generating set
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
that clearly exhibits the permutation structure as described by a stabilizer chain. A stabilizer chain is a sequence of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, each containing the next and each stabilizing one more point.
Let
 be a group of permutations
be a group of permutationsPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
of the set
 Let
Let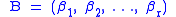
be a sequence of distinct integers,
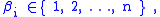 such that the pointwise stabilizer
such that the pointwise stabilizerGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of
 is trivial (i.e., let
is trivial (i.e., let  be a base
be a baseBase (group theory)
Let G be a finite permutation group acting on a set \Omega. A sequenceB = [\beta_1,\beta_2,...,\beta_k]of k distinct elements of \Omega is a base for G if the only element of G which fixes every \beta_i \in B pointwise is the identity element of G....
for
 ). Define
). Define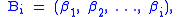
and define
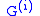 to be the pointwise stabilizer of
to be the pointwise stabilizer of 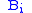 . A strong generating set (SGS) for G relative to the base
. A strong generating set (SGS) for G relative to the base  is a set
is a set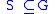
such that
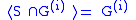
for each
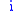 such that
such that 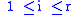 .
.The base and the SGS are said to be non-redundant if
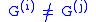
for
 .
.A base and strong generating set (BSGS) for a group can be computed using the Schreier–Sims algorithm.

