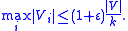Graph partition
Encyclopedia
In mathematics, the graph partition problem is defined on data represented in the form of a graph
G= (V,E), with V vertices and E edges, such that it is possible to partition G into smaller components with specific properties. For instance, a k-way partition divides the vertex set into k smaller components. A good partition is defined such that the number of edges running between separated components is small. Uniform graph partition is a type of graph partitioning problem that consists of dividing a graph into components, such that the components are of about the same size and there are few connections between the components. Important applications of graph partitioning include scientific computing, partitioning various stages of a VLSI design circuit and task scheduling in multi-processor systems. Recently, the uniform graph partition problem has gained importance due to its application for clustering and detection of cliques in social, pathological and biological networks.
s, where an edge can connect more than two vertices. A hyperedge is not cut if all vertices are in one partition, and cut exactly once otherwise, no matter how many vertices are on each side. This usage is common in electronic design automation
.
We already know that (2,1) cut is the minimum bisection problem and it is NP complete. Next we assess a 3-partition problem wherein n=3k, which is also bounded in polynomial time. Now, if we assume that we have an finite approximation algorithm for (k, 1)-balanced partition, then, either the 3-partition instance can be solved using the balanced (k,1) partition in G or it cannot be solved. If the 3-Partition instance can be solved, then (k, 1)-balanced partitioning problem in G can be solved without cutting any edge. Otherwise if the 3-Partition instance cannot be solved, the optimum (k, 1)-balanced partitioning in G will cut at least one edge. An approximation algorithm with finite approximation factor has to differentiate between these two cases. Hence, it can solve the 3-Partition problem which is a contradiction under the assumption that P=NP. Thus, it is evident that (k,1)-balanced partitioning problem has no polynomial time approximation algorithm with finite approximation factor unless P=NP.
The planar separator theorem
states that any n-vertex planar graph
can be partitioned into roughly equal parts by the removal of O(√n) vertices. This is not a partition in the sense described above, because the partition set consists of vertices rather than edges. However, the same result also implies that every planar graph of bounded degree has a balanced cut with O(√n) edges.
Global approaches such as the Spectral partitioning, is based on the spectra of the adjacency matrices.
the graph by collapsing vertices and edges, partitions the smaller graph, then maps back and refines this partition of the original graph. A wide variety of partitioning and refinement methods can be applied within the overall multi-level scheme. In many cases, this approach can give both fast execution times and very high quality results.
One widely used example of such an approach is METIS, a graph partitioner, and hMETIS, the corresponding partitioner for hypergraphs.
In such a scenario, the second smallest eigenvalue (λ) of L, yields a lower bound on the optimal cost (c) of ratio-cut partition with c≥λ/n. The eigenvector (V) corresponding to λ, called the Fiedler vector, bisects the graph into only 2 communities based on the sign of the corresponding vector entry. Division into a larger number of communities is usually achieved by repeated bisection, but this does not always give satisfactory results. The examples in Figures 1,2 illustrate the spectral bisection approach.
Minimum cut partitioning however fails when the number of communities to be partitioned, or the partition sizes are unknown. For instance, optimizing the cut size for free group sizes puts all vertices in the same community. Additionally, cut size may be the wrong thing to minimize since a good division is not just one with small number of edges between communities. This motivated the use of Modularity (networks)
(Q) as a metric to optimize a balanced graph partition. The example in Figure 3 illustrates 2 instances of the same graph such that in (a) modularity (Q) is the partitioning metric and in (b), ratio-cut is the partitioning metric.
(H) is derived by assigning the following partition rewards and penalties.
Additionally, Kernel PCA based Spectral clustering takes a form of least squares Support Vector Machine framework, and hence it becomes possible to project the data entries to a kernel induced feature space that has maximal variance, thus implying a high separation between the projected communities
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
G= (V,E), with V vertices and E edges, such that it is possible to partition G into smaller components with specific properties. For instance, a k-way partition divides the vertex set into k smaller components. A good partition is defined such that the number of edges running between separated components is small. Uniform graph partition is a type of graph partitioning problem that consists of dividing a graph into components, such that the components are of about the same size and there are few connections between the components. Important applications of graph partitioning include scientific computing, partitioning various stages of a VLSI design circuit and task scheduling in multi-processor systems. Recently, the uniform graph partition problem has gained importance due to its application for clustering and detection of cliques in social, pathological and biological networks.
Problem Complexity
Typically, graph partition problems fall under the category of NP-hard problems. Solutions to these problems are generally derived using heuristics and approximation algorithms. However, uniform graph partitioning or a balanced graph partition problem can be shown to be NP-complete.Problem
Consider a graph G=(V, E), where V denotes the set of n vertices and E the set of edges. For a (k,v) balanced partition problem, the objective is to partition G into k components of at most size v.(n/k), while minimizing the capacity of the edges between separate components. Also, given G and an integer k > 1, partition V into k parts (subsets) V1, V2, ..., Vk such that the parts are disjoint and have equal size, and the number of edges with endpoints in different parts is minimized. Such partition problems have been discussed in literature as bacteria-approximation or resource augmentation approaches. A common extension is to hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s, where an edge can connect more than two vertices. A hyperedge is not cut if all vertices are in one partition, and cut exactly once otherwise, no matter how many vertices are on each side. This usage is common in electronic design automation
Electronic design automation
Electronic design automation is a category of software tools for designing electronic systems such as printed circuit boards and integrated circuits...
.
Analysis
For a specific (k,1+ε) balanced partition problem, we seek to find a minimum cost partition of G into k components with each component containing maximum of (1+ε)*(n/k) nodes. We compare the cost of this approximation algorithm to the cost of a (k,1) cut, wherein each of the k components must have exactly the same size of (n/k) nodes each, thus being a more restricted problem. Thus,We already know that (2,1) cut is the minimum bisection problem and it is NP complete. Next we assess a 3-partition problem wherein n=3k, which is also bounded in polynomial time. Now, if we assume that we have an finite approximation algorithm for (k, 1)-balanced partition, then, either the 3-partition instance can be solved using the balanced (k,1) partition in G or it cannot be solved. If the 3-Partition instance can be solved, then (k, 1)-balanced partitioning problem in G can be solved without cutting any edge. Otherwise if the 3-Partition instance cannot be solved, the optimum (k, 1)-balanced partitioning in G will cut at least one edge. An approximation algorithm with finite approximation factor has to differentiate between these two cases. Hence, it can solve the 3-Partition problem which is a contradiction under the assumption that P=NP. Thus, it is evident that (k,1)-balanced partitioning problem has no polynomial time approximation algorithm with finite approximation factor unless P=NP.
Graph Partition Methods
Since graph partitioning is a hard problem, the solutions are based on heuristics. There are two broad categories of these partitioning approaches. While the first one works locally, the second one considers global connectivity. Well known classical methods for partitioning are the Kernighan–Lin algorithm, and Fiduccia-Mattheyses algorithm which were the first effective 2-way cuts by local search strategies. The major drawback was the arbitrary initial partitioning of the vertex set.The planar separator theorem
Planar separator theorem
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices...
states that any n-vertex planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
can be partitioned into roughly equal parts by the removal of O(√n) vertices. This is not a partition in the sense described above, because the partition set consists of vertices rather than edges. However, the same result also implies that every planar graph of bounded degree has a balanced cut with O(√n) edges.
Global approaches such as the Spectral partitioning, is based on the spectra of the adjacency matrices.
Multi-level Methods
A multi-level graph partitioning algorithm works by applying one or more stages. Each stage reduces the size ofthe graph by collapsing vertices and edges, partitions the smaller graph, then maps back and refines this partition of the original graph. A wide variety of partitioning and refinement methods can be applied within the overall multi-level scheme. In many cases, this approach can give both fast execution times and very high quality results.
One widely used example of such an approach is METIS, a graph partitioner, and hMETIS, the corresponding partitioner for hypergraphs.
Spectral Partitioning/Spectral Bisection
Given a graph with adjacency matrix A, where an entry Aij implies an edge between node i and j, and degree matrix D, which is a diagonal matrix, where each diagonal entry of a row i, dii, represents the node degree of node i. The Laplacian of the matrix A is defined as L=D-A. Now, a ratio-cut partition for graph G=(V,E) is defined as a partition of V into disjoint U, and W, such that cost of cut(U,W)/(|U|.|W|) is minimized.In such a scenario, the second smallest eigenvalue (λ) of L, yields a lower bound on the optimal cost (c) of ratio-cut partition with c≥λ/n. The eigenvector (V) corresponding to λ, called the Fiedler vector, bisects the graph into only 2 communities based on the sign of the corresponding vector entry. Division into a larger number of communities is usually achieved by repeated bisection, but this does not always give satisfactory results. The examples in Figures 1,2 illustrate the spectral bisection approach.
Minimum cut partitioning however fails when the number of communities to be partitioned, or the partition sizes are unknown. For instance, optimizing the cut size for free group sizes puts all vertices in the same community. Additionally, cut size may be the wrong thing to minimize since a good division is not just one with small number of edges between communities. This motivated the use of Modularity (networks)
Modularity (networks)
Modularity is one measure of the structure of networks or graphs. It measures the strength of division of a network into modules . Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules...
(Q) as a metric to optimize a balanced graph partition. The example in Figure 3 illustrates 2 instances of the same graph such that in (a) modularity (Q) is the partitioning metric and in (b), ratio-cut is the partitioning metric.
Other Graph Partition Methods
Spin models have used for clustering of multivariate data wherein similarities are translated into coupling strengths. The properties of ground state spin configuration can be directly interpreted as communities. Thus, a graph is partitioned to minimize the Hamiltonian of the partitioned graph. The HamiltonianHamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
(H) is derived by assigning the following partition rewards and penalties.
- Reward internal edges between nodes of same group (same spin)
- Penalize missing edges in same group
- Penalize existing edges between different groups
- Reward non-links between different groups.
Additionally, Kernel PCA based Spectral clustering takes a form of least squares Support Vector Machine framework, and hence it becomes possible to project the data entries to a kernel induced feature space that has maximal variance, thus implying a high separation between the projected communities