
Stopped process
Encyclopedia
In mathematics
, a stopped process is a stochastic process
that is forced to assume the same value after a prescribed (possibly random) time.
Then the stopped process is defined for
is defined for  and
and 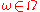 by
by
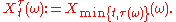
. Xt denotes the gambler's total holdings in the casino at time t ≥ 0, which may or may not be allowed to be negative, depending on whether or not the casino offers credit. Let Yt denote what the gambler's holdings would be if he/she could obtain unlimited credit (so Y can attain negative values).

is a stopping time for Y, and, since the gambler cannot continue to play after he/she has exhausted his/her resources, X is the stopped process Yτ.
 be a one-dimensional standard Brownian motion
be a one-dimensional standard Brownian motion
starting at zero.
Then the stopped Brownian motion will evolve as per usual up until the random time
will evolve as per usual up until the random time  , and will thereafter be constant with value
, and will thereafter be constant with value  : i.e.,
: i.e., 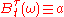 for all
for all  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a stopped process is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
that is forced to assume the same value after a prescribed (possibly random) time.
Definition
Let-
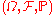 be a probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
be a probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
; -
 be a measurable space;
be a measurable space; -
 be a stochastic process;
be a stochastic process; -
 be a stopping timeStopping ruleIn probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”....
be a stopping timeStopping ruleIn probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”....
with respect to some filtrationFiltration (abstract algebra)In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
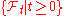 of
of  .
.
Then the stopped process
 is defined for
is defined for  and
and 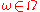 by
by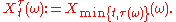
Gambling
Consider a gambler playing rouletteRoulette
Roulette is a casino game named after a French diminutive for little wheel. In the game, players may choose to place bets on either a single number or a range of numbers, the colors red or black, or whether the number is odd or even....
. Xt denotes the gambler's total holdings in the casino at time t ≥ 0, which may or may not be allowed to be negative, depending on whether or not the casino offers credit. Let Yt denote what the gambler's holdings would be if he/she could obtain unlimited credit (so Y can attain negative values).
- Stopping at a deterministic time: suppose that the casino is prepared to lend the gambler unlimited credit, and that the gambler resolves to leave the game at a predetermined time T, regardless of the state of play. Then X is really the stopped process YT, since the gambler's account remains in the same state after leaving the game as it was in at the moment that the gambler left the game.
- Stopping at a random time: suppose that the gambler has no other sources of revenue, and that the casino will not extend its customers credit. The gambler resolves to play until and unless he/she goes broke. Then the random time

is a stopping time for Y, and, since the gambler cannot continue to play after he/she has exhausted his/her resources, X is the stopped process Yτ.
Brownian motion
Let be a one-dimensional standard Brownian motion
be a one-dimensional standard Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
starting at zero.
- Stopping at a deterministic time
 : if
: if 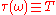 , then the stopped Brownian motion
, then the stopped Brownian motion  will evolve as per usual up until time
will evolve as per usual up until time  , and thereafter will stay constant: i.e.,
, and thereafter will stay constant: i.e., 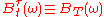 for all
for all  .
.
- Stopping at a random time: define a random stopping time
 by the first hitting timeHitting timeIn the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
by the first hitting timeHitting timeIn the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
for the region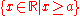 :
:
Then the stopped Brownian motion
 will evolve as per usual up until the random time
will evolve as per usual up until the random time  , and will thereafter be constant with value
, and will thereafter be constant with value  : i.e.,
: i.e., 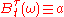 for all
for all  .
.


