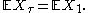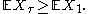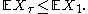Optional stopping theorem
Encyclopedia
In probability theory
, the optional stopping theorem (or Doob's optional sampling theorem) says that, under certain conditions, the expected value
of a martingale
at a stopping time is equal to its initial value (and also expected value at any deterministic time). One version of the theorem is given below:
 denote the stopped process
denote the stopped process
. This is also a martingale (or a submartingale/supermartingale accordingly). Obviously it converges to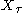 almost surely. Now writing the stopped process as
almost surely. Now writing the stopped process as
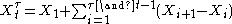
gives
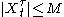 where
where 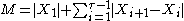 .
.
Now by the monotone convergence theorem
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the optional stopping theorem (or Doob's optional sampling theorem) says that, under certain conditions, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of a martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
at a stopping time is equal to its initial value (and also expected value at any deterministic time). One version of the theorem is given below:
- Let X1, X2, X3, ... be a martingale and τ a stopping time with respect to X1, X2, X3, ... . If
-
- (a)
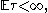
- (a)
- and
-
- (b) there exists a constantMathematical constantA mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
c such that a.s. for all i,
a.s. for all i,
- (b) there exists a constant
- then
- Similarly, if X1, X2, X3, ... is a submartingales or a supermartingales and the above conditions hold then
- for a submartingales, and
- for a supermartingales.
Applications
- The optional stopping theorem can be used to prove the impossibility of successful betting strategies for a gambler with a finite lifetime (which gives condition (a)) and a house limit on bets (condition (b)). Suppose that the gambler can wager up to c dollars on a fair coin flip at times 1, 2, 3, etc., winning his wager if the coin comes up heads and losing it if the coin comes up tails. Suppose further that he can quit whenever he likes, but cannot predict the outcome of gambles that haven't happened yet. Then the gambler's fortune over time is a martingale, and the time τ at which he decides to quit (or goes broke and is forced to quit) is a stopping time. So the theorem says that E[Xτ] = E[X1]. In other words, the gambler leaves with the same amount of money on average as when he started. (The same result holds if the gambler, instead of having a house limit on individual bets, has a finite limit on his line of credit or how far in debt he may go, though this is easier to show with another version of the theorem.)
- Suppose a random walkRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
that goes up or down by one with equal probability on each step. Suppose further that the walk stops if it reaches 0 or m; the time at which this first occurs is a stopping time. If it is known that the expected time at which the walk ends is finite (say, from Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
theory), the optional stopping theorem predicts that the expected stop position is equal to the initial position a. Solving a = pm + (1 − p)0 for the probability p that the walk reaches m before 0 gives p = a/m.
- Now consider a random walk that starts at 0 and stops if it reaches −m or +m, and use the Yn = Xn2 − n martingale from the examples section. If τ is the time at which it first reaches ±m, then 0 = E[Y1] = E[Yτ] = m2 − E[τ]. This gives E[τ] = m2.
- Care must be taken, however, to ensure that all the conditions of theorem hold. For example, suppose the last example had instead used a 'one-sided' stopping time, so that stopping only occurred at +m, not at −m. The value of X at this stopping time would therefore be m. Therefore, the expectation value E[Xτ] must also be m, seemingly in violation of the theorem which would require E[Xτ]=0. The failure of the optional stopping theorem shows that the expected time for the random walk to exceed any non-zero level must be infinite.
Proof
Assume the conditions in the version given above and let denote the stopped process
denote the stopped processStopped process
In mathematics, a stopped process is a stochastic process that is forced to assume the same value after a prescribed time.-Definition:Let* be a probability space;...
. This is also a martingale (or a submartingale/supermartingale accordingly). Obviously it converges to
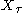 almost surely. Now writing the stopped process as
almost surely. Now writing the stopped process as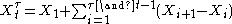
gives
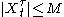 where
where 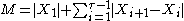 .
.Now by the monotone convergence theorem
-
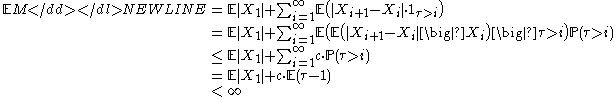
so since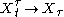 a.s., by the dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
a.s., by the dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
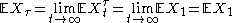 . Similarly, the appropriate inequality is reached for a submartingale/supermartingale by changing the middle equality to an inequality.
. Similarly, the appropriate inequality is reached for a submartingale/supermartingale by changing the middle equality to an inequality.