
Statistical potential
Encyclopedia
In protein structure prediction
, a statistical potential or knowledge-based potential is an energy function derived from an analysis of known protein structures in the Protein Data Bank
.
Many methods exist to obtain such potentials; two notable method are the quasi-chemical approximation (due to Miyazawa and Jernigan ) and the potential of mean force (due to Sippl ). Although the obtained energies are often considered as approximations of the free energy
, this physical interpretation is highly disputed. Nonetheless, they have been applied with great success, and do have a rigorous probabilistic justification.
 angles of the Ramachandran plot
angles of the Ramachandran plot
), solvent exposure or hydrogen bond
geometry. The classic application of such potentials is however pairwise amino acid contacts or distances. For pairwise amino acid contacts, a statistical potential is formulated as an interaction matrix
that assigns a weight or energy value to each possible pair of standard amino acids. The energy of a particular structural model is then the combined energy of all pairwise contacts (defined as two amino acids within a certain distance of each other) in the structure. The energies are determined using statistics on amino acid contacts in a database of known protein structures (obtained from the Protein Data Bank
).
, as applied to pairwise distances between amino acids. This is incorrect, but a useful start to introduce the construction of the potential in practice.
The Boltzmann distribution applied to a specific pair of amino acids,
is given by:

where is the distance,
is the distance,  is the Boltzmann constant,
is the Boltzmann constant,  is
is
the temperature and is the partition function
is the partition function
, with
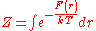
The quantity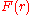 is the free energy assigned to the pairwise system.
is the free energy assigned to the pairwise system.
Simple rearrangement results in the inverse Boltzmann formula,
which expresses the free energy as a function of
as a function of  :
:
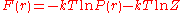
To construct a PMF, one then introduces a so-called reference
state with a corresponding distribution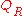 and partition function
and partition function
 , and calculates the following free energy difference:
, and calculates the following free energy difference:

The reference state typically results from a hypothetical
system in which the specific interactions between the amino acids
are absent. The second term involving and
and
 can be ignored, as it is a constant.
can be ignored, as it is a constant.
In practice, is estimated from the database of known protein
is estimated from the database of known protein
structures, while typically results from calculations
typically results from calculations
or simulations. For example,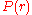 could be the conditional probability
could be the conditional probability
of finding the atoms of a valine and a serine at a given
atoms of a valine and a serine at a given
distance from each other, giving rise to the free energy difference
from each other, giving rise to the free energy difference
 . The total free energy difference of a protein,
. The total free energy difference of a protein,
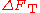 , is then claimed to be the sum
, is then claimed to be the sum
of all the pairwise free energies:
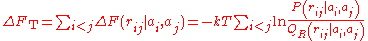
where the sum runs over all amino acid pairs
(with ) and
) and 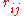 is their corresponding distance. It should
is their corresponding distance. It should
be noted that in many studies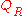 does not depend on the amino
does not depend on the amino
acid sequence .
Intuitively, it is clear that a low value for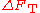 indicates
indicates
that the set of distances in a structure is more likely in proteins than
in the reference state. However, the physical meaning of these PMFs have
been widely disputed since their introduction. The main issues are the interpretation of this "potential" as a true, physically valid potential of mean force
, the nature of the reference state and its optimal formulation, and the validity of generalizations beyond pairwise distances.
based on an analogy with the statistical physics of liquids.
For liquids ,
the potential of mean force is related to the radial distribution function
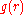 , which is given by:
, which is given by:
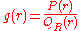
where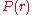 and
and 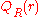 are the respective probabilities of
are the respective probabilities of
finding two particles at a distance from each other in the liquid
from each other in the liquid
and in the reference state. For liquids, the reference state
is clearly defined; it corresponds to the ideal gas, consisting of
non-interacting particles. The two-particle potential of mean force
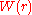 is related to
is related to  by:
by:
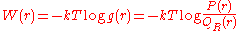
According to the reversible work theorem, the two-particle
potential of mean force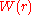 is the reversible work required to
is the reversible work required to
bring two particles in the liquid from infinite separation to a distance
 from each other.
from each other.
Sippl justified the use of PMFs - a few years after he introduced
them for use in protein structure prediction - by
appealing to the analogy with the reversible work theorem for liquids. For liquids,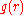 can be experimentally measured
can be experimentally measured
using small angle X-ray scattering; for proteins, is obtained
is obtained
from the set of known protein structures, as explained in the previous
section. However, as Ben-Naim writes in a publication on the subject :
Another issue is that the analogy does not specify
a suitable reference state for proteins.
Bayesian point of view and used these insights in the construction of
the coarse grained ROSETTA energy function. According
to Bayesian probability calculus, the conditional probability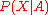 of a structure
of a structure  , given the amino acid sequence
, given the amino acid sequence  , can be
, can be
written as:

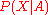 is proportional to the product of
is proportional to the product of
the likelihood times the prior
times the prior
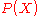 . By assuming that the likelihood can be approximated
. By assuming that the likelihood can be approximated
as a product of pairwise probabilities, and applying Bayes' theorem, the
likelihood can be written as:
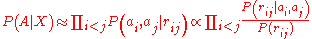
where the product runs over all amino acid pairs (with
(with
 ), and
), and  is the distance between amino acids
is the distance between amino acids  and
and 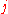 .
.
Obviously, the negative of the logarithm of the expression
has the same functional form as the classic
pairwise distance PMFs, with the denominator playing the role of the
reference state. This explanation has two shortcomings: it is purely qualitative,
and relies on the unfounded assumption the likelihood can be expressed
as a product of pairwise probabilities.
probability theory to solve a fundamental problem that arises in protein
structure prediction: how to improve an imperfect probability
distribution over a first variable
over a first variable  using a probability
using a probability
distribution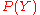 over a second variable
over a second variable  , with
, with  . Typically,
. Typically,  and
and  are fine and coarse grained variables, respectively. For example,
are fine and coarse grained variables, respectively. For example, 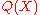 could concern
could concern
the local structure of the protein, while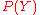 could concern the pairwise distances between the amino acids. In that case,
could concern the pairwise distances between the amino acids. In that case,  could for example be a vector of dihedral angles that specifies all atom positions (assuming ideal bond lengths and angles).
could for example be a vector of dihedral angles that specifies all atom positions (assuming ideal bond lengths and angles).
In order to combine the two distributions, such that the local structure will be distributed according to , while
, while
the pairwise distances will be distributed according to , the following expression is needed:
, the following expression is needed:
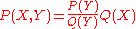
where is the distribution over
is the distribution over  implied by
implied by  . The ratio in the expression corresponds
. The ratio in the expression corresponds
to the PMF. Typically, is brought in by sampling (typically from a fragment library), and not explicitly evaluated; the ratio, which in contrast is explicitly evaluated, corresponds to Sippl's potential of mean force. This explanation is quantitive, and allows the generalization of PMFs from pairwise distances to arbitrary coarse grained variables. It also
is brought in by sampling (typically from a fragment library), and not explicitly evaluated; the ratio, which in contrast is explicitly evaluated, corresponds to Sippl's potential of mean force. This explanation is quantitive, and allows the generalization of PMFs from pairwise distances to arbitrary coarse grained variables. It also
provides a rigorous definition of the reference state, which is implied by . Conventional applications of pairwise distance PMFs usually lack two
. Conventional applications of pairwise distance PMFs usually lack two
necessary features to make them fully rigorous: the use of a proper probability distribution over pairwise distances in proteins, and the recognition that the reference state is rigorously
defined by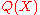 .
.
or protein threading - predictions for the tertiary structure assumed by a particular amino acid sequence made on the basis of comparisons to one or more homologous
proteins with known structure. Many differently parameterized statistical potentials have been shown to successfully identify the native state structure from an ensemble of "decoy" or non-native structures. Statistical potentials are not only used for protein structure prediction
, but also for modelling the protein folding
pathway .
Protein structure prediction
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse...
, a statistical potential or knowledge-based potential is an energy function derived from an analysis of known protein structures in the Protein Data Bank
Protein Data Bank
The Protein Data Bank is a repository for the 3-D structural data of large biological molecules, such as proteins and nucleic acids....
.
Many methods exist to obtain such potentials; two notable method are the quasi-chemical approximation (due to Miyazawa and Jernigan ) and the potential of mean force (due to Sippl ). Although the obtained energies are often considered as approximations of the free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
, this physical interpretation is highly disputed. Nonetheless, they have been applied with great success, and do have a rigorous probabilistic justification.
Assigning an energy
Possible features to which an energy can be assigned include torsion angles (such as the angles of the Ramachandran plot
angles of the Ramachandran plotRamachandran plot
-Introduction and early history:A Ramachandran plot , originally developed in 1963 by G. N. Ramachandran C. Ramakrishnan and V...
), solvent exposure or hydrogen bond
Hydrogen bond
A hydrogen bond is the attractive interaction of a hydrogen atom with an electronegative atom, such as nitrogen, oxygen or fluorine, that comes from another molecule or chemical group. The hydrogen must be covalently bonded to another electronegative atom to create the bond...
geometry. The classic application of such potentials is however pairwise amino acid contacts or distances. For pairwise amino acid contacts, a statistical potential is formulated as an interaction matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that assigns a weight or energy value to each possible pair of standard amino acids. The energy of a particular structural model is then the combined energy of all pairwise contacts (defined as two amino acids within a certain distance of each other) in the structure. The energies are determined using statistics on amino acid contacts in a database of known protein structures (obtained from the Protein Data Bank
Protein Data Bank
The Protein Data Bank is a repository for the 3-D structural data of large biological molecules, such as proteins and nucleic acids....
).
Overview
Many textbooks present the potentials of mean force (PMFs) as proposed by Sippl as a simple consequence of the Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
, as applied to pairwise distances between amino acids. This is incorrect, but a useful start to introduce the construction of the potential in practice.
The Boltzmann distribution applied to a specific pair of amino acids,
is given by:

where
 is the distance,
is the distance,  is the Boltzmann constant,
is the Boltzmann constant,  is
isthe temperature and
 is the partition function
is the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
, with
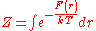
The quantity
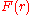 is the free energy assigned to the pairwise system.
is the free energy assigned to the pairwise system.Simple rearrangement results in the inverse Boltzmann formula,
which expresses the free energy
 as a function of
as a function of  :
: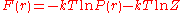
To construct a PMF, one then introduces a so-called reference
state with a corresponding distribution
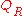 and partition function
and partition function , and calculates the following free energy difference:
, and calculates the following free energy difference:
The reference state typically results from a hypothetical
system in which the specific interactions between the amino acids
are absent. The second term involving
 and
and can be ignored, as it is a constant.
can be ignored, as it is a constant.In practice,
 is estimated from the database of known protein
is estimated from the database of known proteinstructures, while
 typically results from calculations
typically results from calculationsor simulations. For example,
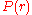 could be the conditional probability
could be the conditional probabilityof finding the
 atoms of a valine and a serine at a given
atoms of a valine and a serine at a givendistance
 from each other, giving rise to the free energy difference
from each other, giving rise to the free energy difference . The total free energy difference of a protein,
. The total free energy difference of a protein,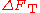 , is then claimed to be the sum
, is then claimed to be the sumof all the pairwise free energies:
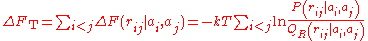
where the sum runs over all amino acid pairs

(with
 ) and
) and 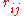 is their corresponding distance. It should
is their corresponding distance. It shouldbe noted that in many studies
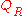 does not depend on the amino
does not depend on the aminoacid sequence .
Intuitively, it is clear that a low value for
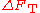 indicates
indicatesthat the set of distances in a structure is more likely in proteins than
in the reference state. However, the physical meaning of these PMFs have
been widely disputed since their introduction. The main issues are the interpretation of this "potential" as a true, physically valid potential of mean force
Potential of mean force
The Potential of Mean Force of a system with N molecules is strictly the potential that gives the average force over all the configurations of all the n+1...N molecules acting on a particle at any fixed configuration keeping fixed a set of molecules 1...n...
, the nature of the reference state and its optimal formulation, and the validity of generalizations beyond pairwise distances.
Analogy with liquid systems
The first, qualitative justification of PMFs is due to Sippl, andbased on an analogy with the statistical physics of liquids.
For liquids ,
the potential of mean force is related to the radial distribution function
Radial distribution function
In statistical mechanics, a radial distribution function , g, describes how the atomic density varies as a function of the distance from one particular atom....
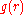 , which is given by:
, which is given by: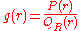
where
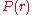 and
and 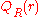 are the respective probabilities of
are the respective probabilities offinding two particles at a distance
 from each other in the liquid
from each other in the liquidand in the reference state. For liquids, the reference state
is clearly defined; it corresponds to the ideal gas, consisting of
non-interacting particles. The two-particle potential of mean force
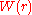 is related to
is related to  by:
by: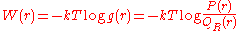
According to the reversible work theorem, the two-particle
potential of mean force
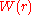 is the reversible work required to
is the reversible work required tobring two particles in the liquid from infinite separation to a distance
 from each other.
from each other. Sippl justified the use of PMFs - a few years after he introduced
them for use in protein structure prediction - by
appealing to the analogy with the reversible work theorem for liquids. For liquids,
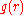 can be experimentally measured
can be experimentally measuredusing small angle X-ray scattering; for proteins,
 is obtained
is obtainedfrom the set of known protein structures, as explained in the previous
section. However, as Ben-Naim writes in a publication on the subject :
[...]the quantities, referred to as `statistical potentials,' `structure
based potentials,' or `pair potentials of mean force', as derived from
the protein data bank, are neither `potentials' nor `potentials of
mean force,' in the ordinary sense as used in the literature on
liquids and solutions.
Another issue is that the analogy does not specify
a suitable reference state for proteins.
Analogy with likelihood
Baker and co-workers justified PMFs from aBayesian point of view and used these insights in the construction of
the coarse grained ROSETTA energy function. According
to Bayesian probability calculus, the conditional probability
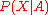 of a structure
of a structure  , given the amino acid sequence
, given the amino acid sequence  , can be
, can bewritten as:

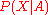 is proportional to the product of
is proportional to the product ofthe likelihood
 times the prior
times the prior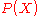 . By assuming that the likelihood can be approximated
. By assuming that the likelihood can be approximatedas a product of pairwise probabilities, and applying Bayes' theorem, the
likelihood can be written as:
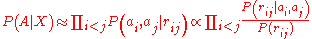
where the product runs over all amino acid pairs
 (with
(with ), and
), and  is the distance between amino acids
is the distance between amino acids  and
and 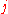 .
.Obviously, the negative of the logarithm of the expression
has the same functional form as the classic
pairwise distance PMFs, with the denominator playing the role of the
reference state. This explanation has two shortcomings: it is purely qualitative,
and relies on the unfounded assumption the likelihood can be expressed
as a product of pairwise probabilities.
Reference ratio explanation
Expressions that resemble PMFs naturally result from the application ofprobability theory to solve a fundamental problem that arises in protein
structure prediction: how to improve an imperfect probability
distribution
 over a first variable
over a first variable  using a probability
using a probabilitydistribution
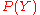 over a second variable
over a second variable  , with
, with  . Typically,
. Typically,  and
and  are fine and coarse grained variables, respectively. For example,
are fine and coarse grained variables, respectively. For example, 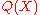 could concern
could concernthe local structure of the protein, while
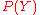 could concern the pairwise distances between the amino acids. In that case,
could concern the pairwise distances between the amino acids. In that case,  could for example be a vector of dihedral angles that specifies all atom positions (assuming ideal bond lengths and angles).
could for example be a vector of dihedral angles that specifies all atom positions (assuming ideal bond lengths and angles).In order to combine the two distributions, such that the local structure will be distributed according to
 , while
, whilethe pairwise distances will be distributed according to
 , the following expression is needed:
, the following expression is needed: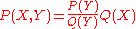
where
 is the distribution over
is the distribution over  implied by
implied by  . The ratio in the expression corresponds
. The ratio in the expression correspondsto the PMF. Typically,
 is brought in by sampling (typically from a fragment library), and not explicitly evaluated; the ratio, which in contrast is explicitly evaluated, corresponds to Sippl's potential of mean force. This explanation is quantitive, and allows the generalization of PMFs from pairwise distances to arbitrary coarse grained variables. It also
is brought in by sampling (typically from a fragment library), and not explicitly evaluated; the ratio, which in contrast is explicitly evaluated, corresponds to Sippl's potential of mean force. This explanation is quantitive, and allows the generalization of PMFs from pairwise distances to arbitrary coarse grained variables. It alsoprovides a rigorous definition of the reference state, which is implied by
 . Conventional applications of pairwise distance PMFs usually lack two
. Conventional applications of pairwise distance PMFs usually lack twonecessary features to make them fully rigorous: the use of a proper probability distribution over pairwise distances in proteins, and the recognition that the reference state is rigorously
defined by
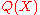 .
.Applications
Statistical potentials are used as energy functions in the assessment of an ensemble of structural models produced by homology modelingHomology modeling
Homology modeling, also known as comparative modeling of protein refers to constructing an atomic-resolution model of the "target" protein from its amino acid sequence and an experimental three-dimensional structure of a related homologous protein...
or protein threading - predictions for the tertiary structure assumed by a particular amino acid sequence made on the basis of comparisons to one or more homologous
Homology (biology)
Homology forms the basis of organization for comparative biology. In 1843, Richard Owen defined homology as "the same organ in different animals under every variety of form and function". Organs as different as a bat's wing, a seal's flipper, a cat's paw and a human hand have a common underlying...
proteins with known structure. Many differently parameterized statistical potentials have been shown to successfully identify the native state structure from an ensemble of "decoy" or non-native structures. Statistical potentials are not only used for protein structure prediction
Protein structure prediction
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse...
, but also for modelling the protein folding
Protein folding
Protein folding is the process by which a protein structure assumes its functional shape or conformation. It is the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure from random coil....
pathway .

