Star height problem
Encyclopedia
The star height problem in formal language theory is the question whether all regular language
s can be expressed using regular expressions of limited star height
, i.e. with a limited nesting depth of Kleene star
s. Specifically, is a nesting depth of one always sufficient? If not, is there an algorithm
to determine how many are required? The problem was raised by .
n for every n. Here, the star height h(L) of a regular language L is defined as the minimum star height among all regular expressions representing L. The first few languages found by are described in the following, by means of giving a regular expression for each language:
The construction principle for these expressions is that expression
is obtained by concatening two copies of 
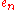, appropriately renaming the letters of the second copy using fresh alphabet symbols, concatenating the result with another fresh alphabet symbol, and then by surrounding the resulting expression with a Kleene star. The remaining, more difficult part, is to prove that for 
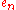there is no equivalent regular expression of star height less than n; a proof is given in .
However, Eggan's examples use a large alphabet, of size 2n-1 for the language with star height n. He thus asked whether we can also find examples over binary alphabets. This was proved to be true shortly afterwards by .
Their examples can be described by an inductively defined family of regular expressions over the binary alphabet
as follows–cf. :
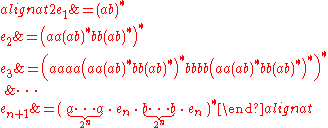
Again, a rigorous proof is needed for the fact that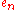
does not admit an equivalent regular expression of lower star height. Proofs are given by and by .
. But the general problem remained open for more than 25 years until it was settled by Hashiguchi, who in 1988 published an algorithm to determine the star height
of any regular language. The algorithm wasn't at all practical, being of non-elementary complexity. To illustrate the immense resource consumptions of that algorithm, Lombardy and Sakarovitch (2002) give some actual numbers:
Notice that alone the number
has 10 billion zeros when written down in decimal notation, and is already by far larger than the number of atoms in the observable universe.
A much more efficient algorithm than Hashiguchi's procedure was devised by Kirsten in 2005. This algorithm runs, for a given nondeterministic finite automaton
as input, within double-exponential space
. Yet the resource requirements of this algorithm still greatly exceed the margins of what is considered practically feasible.
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s can be expressed using regular expressions of limited star height
Star height
In theoretical computer science, more precisely in the theory of formal languages, the star height is a measure for the structural complexityof regular expressions: The star height equals the maximum nesting depth of stars appearing in the regular expression....
, i.e. with a limited nesting depth of Kleene star
Kleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
s. Specifically, is a nesting depth of one always sufficient? If not, is there an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to determine how many are required? The problem was raised by .
Families of regular languages with unbounded star height
The first question was answered in the negative when in 1963, Eggan gave examples of regular languages of star heightStar height
In theoretical computer science, more precisely in the theory of formal languages, the star height is a measure for the structural complexityof regular expressions: The star height equals the maximum nesting depth of stars appearing in the regular expression....
n for every n. Here, the star height h(L) of a regular language L is defined as the minimum star height among all regular expressions representing L. The first few languages found by are described in the following, by means of giving a regular expression for each language:
The construction principle for these expressions is that expression
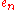is obtained by concatening two copies of , appropriately renaming the letters of the second copy using fresh alphabet symbols, concatenating the result with another fresh alphabet symbol, and then by surrounding the resulting expression with a Kleene star. The remaining, more difficult part, is to prove that for 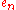there is no equivalent regular expression of star height less than n; a proof is given in .However, Eggan's examples use a large alphabet, of size 2n-1 for the language with star height n. He thus asked whether we can also find examples over binary alphabets. This was proved to be true shortly afterwards by .
Their examples can be described by an inductively defined family of regular expressions over the binary alphabet
as follows–cf. :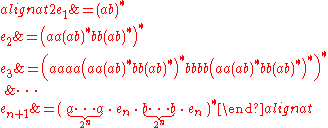Again, a rigorous proof is needed for the fact that
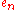does not admit an equivalent regular expression of lower star height. Proofs are given by and by .Computing the star height of regular languages
In contrast, the second question turned out to be much more difficult, and the question became a famous open problem in formal language theory for over two decades . For years, there was only little progress. The pure-group languages were the first interesting family of regular languages for which the star height problem was proved to be decidableDecidable
The word decidable may refer to:* Decidable language*Decidability for the equivalent in mathematical logic*Gödel's incompleteness theorem, a theorem on the indecidability of languages consisting of "true statements" in mathematical logic....
. But the general problem remained open for more than 25 years until it was settled by Hashiguchi, who in 1988 published an algorithm to determine the star height
Star height
In theoretical computer science, more precisely in the theory of formal languages, the star height is a measure for the structural complexityof regular expressions: The star height equals the maximum nesting depth of stars appearing in the regular expression....
of any regular language. The algorithm wasn't at all practical, being of non-elementary complexity. To illustrate the immense resource consumptions of that algorithm, Lombardy and Sakarovitch (2002) give some actual numbers:
Notice that alone the number
has 10 billion zeros when written down in decimal notation, and is already by far larger than the number of atoms in the observable universe.A much more efficient algorithm than Hashiguchi's procedure was devised by Kirsten in 2005. This algorithm runs, for a given nondeterministic finite automaton
Nondeterministic finite state machine
In the automata theory, a nondeterministic finite state machine or nondeterministic finite automaton is a finite state machine where from each state and a given input symbol the automaton may jump into several possible next states...
as input, within double-exponential space
EXPSPACE
In complexity theory, EXPSPACE is the set of all decision problems solvable by a deterministic Turing machine in O space, where p is a polynomial function of n...
. Yet the resource requirements of this algorithm still greatly exceed the margins of what is considered practically feasible.