Nondeterministic finite state machine
Encyclopedia
In the automata theory
, a nondeterministic finite state machine or nondeterministic finite automaton (NFA) is a finite state machine
where from each state and a given input symbol the automaton may jump into several possible next states. This distinguishes it from the deterministic finite automaton (DFA), where the next possible state is uniquely determined.
Although the DFA and NFA have distinct definitions,
a NFA can be translated to equivalent DFA using powerset construction
, i.e.,
the constructed DFA and the NFA recognize the same formal language
.
Both types of automata recognize only regular languages.
Nondeterministic finite automata were introduced in 1959 by Michael O. Rabin
and Dana Scott
, who also showed their equivalence to deterministic finite automata.
Non-deterministic finite state machines are sometimes studied by the name subshifts of finite type. Non-deterministic finite state machines are generalized by probabilistic automata, which assign a probability to each state transition.
Unlike a DFA, it is non-deterministic in that, for any input symbol, its next state may be any one of several possible states. Thus, in the formal definition, the next state is an element of the power set of states. This element, itself a set, represents some subset of all possible states to be considered at once.
The notion of accepting an input is similar to that for the DFA. When the last input symbol is consumed, the NFA accepts if and only if there is some set of transitions that will take it to an accepting state. Equivalently, it rejects, if, no matter what transitions are applied, it would not end in an accepting state.
An extension of the NFA is the NFA-ε (also known as NFA-λ or the NFA with epsilon moves), which allows a transformation to a new state without consuming any input symbols. Transformations to new states without consuming an input symbol are called ε-transitions or λ-transitions. They are usually labeled with the Greek letter ε or λ. For example, if it is in state 1, with the next input symbol an a, it can move to state 2 without consuming any input symbols, and thus there is an ambiguity: is the system in state 1, or state 2, before consuming the letter a? Because of this ambiguity, it is more convenient to talk of the set of possible states the system may be in. Thus, before consuming letter a, the NFA-epsilon may be in any one of the states out of the set {1,2}. Equivalently, one may imagine that the NFA is in state 1 and 2 'at the same time': and this gives an informal hint of the powerset construction
: the DFA equivalent to an NFA is defined as the one that is in the state q={1,2}.
(Q, Σ, Δ, q0, F), consisting of
Here, P(Q) denotes the power set of Q.
Let w = a1a2 ... an be a word over the alphabet Σ. The automaton M accepts the word w if a sequence of states,
r0,r1, ..., rn, exists in Q with the following conditions:
In words, the first condition says that the machine starts in the start state q0. The second condition says that given each character of string w, the machine will transition from state to state according to the transition relation Δ. The last condition says that the machine accepts w if the last input of w causes the machine to halt in one of the accepting states. Otherwise, it is said that the automaton rejects the string. The set of strings M accepts is the language
recognized by M and this language is denoted by L(M).
For more comprehensive introduction of the formal definition see automata theory
.
NFA-ε
The NFA-ε (also sometimes called NFA-λ or NFA with epsilon moves) replaces the transition function with one that allows the empty string
ε as a possible input, so that one has instead
It can be shown that ordinary NFA and NFA-ε are equivalent, in that, given either one, one can construct the other, which recognizes the same language.
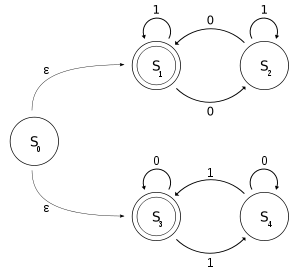Let M be a NFA-epsilon, with a binary alphabet, that determines if the input contains an even number of 0s or an even number of 1s. Note that 0 occurrences is an even number of occurrences as well.
In formal notation, let M = ({s0, s1, s2, s3, s4}, {0, 1}, Δ, s0, {s1, s3}) where
the transition relation T can be defined by this state transition table
:
M can be viewed as the union of two DFA
s: one with states {S1, S2} and the other with states {S3, S4}.
The language of M can be described by the regular language
given by this regular expression
(1*(01*01*)*) ∪ (0*(10*10*)*).
We define M using ε-moves
but M can be defined without using ε-moves.
The set of all strings accepted by an NFA is the language the NFA accepts. This language is a regular language
.
For every NFA a deterministic finite state machine
(DFA) can be found that accepts the same language. Therefore it is possible to convert an existing NFA into a DFA for the purpose of implementing a (perhaps) simpler machine. This can be performed using the powerset construction
, which may lead to an exponential rise in the number of necessary states. A formal proof of the powerset construction is given here.
one writes 
if and only if 
can be reached from 
by going along zero or more 
arrows. In other words, 
if and only if there exists 
where 
such that
For any
, the set of states that can be reached from p is called the epsilon-closure or ε-closure of p, and is written as
For any subset
, define the ε-closure of P as
The ε-transitions are transitive, in that it may be shown that, for all
and 
, if 
and 
, then 
.
Similarly, if
and 
then 
Let x be a string over the alphabet Σ∪{ε}. An NFA-ε M accepts the string x if there exist both a representation of x of the form x1x2 ... xn, where xi ∈ (Σ ∪{ε}), and a sequence of states
p0,p1, ..., pn, where pi ∈ Q, meeting the following conditions:
. For example, it is much easier to prove the following properties using NFAs than DFAs:
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
, a nondeterministic finite state machine or nondeterministic finite automaton (NFA) is a finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
where from each state and a given input symbol the automaton may jump into several possible next states. This distinguishes it from the deterministic finite automaton (DFA), where the next possible state is uniquely determined.
Although the DFA and NFA have distinct definitions,
a NFA can be translated to equivalent DFA using powerset construction
Powerset construction
In the theory of computation and Automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton into a deterministic finite automaton which recognizes the same formal language...
, i.e.,
the constructed DFA and the NFA recognize the same formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
.
Both types of automata recognize only regular languages.
Nondeterministic finite automata were introduced in 1959 by Michael O. Rabin
Michael O. Rabin
Michael Oser Rabin , is an Israeli computer scientist and a recipient of the Turing Award.- Biography :Rabin was born in 1931 in Breslau, Germany, , the son of a rabbi. In 1935, he emigrated with his family to Mandate Palestine...
and Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
, who also showed their equivalence to deterministic finite automata.
Non-deterministic finite state machines are sometimes studied by the name subshifts of finite type. Non-deterministic finite state machines are generalized by probabilistic automata, which assign a probability to each state transition.
Informal introduction
An NFA, similar to a DFA, consumes a string of input symbols. For each input symbol it transitions to a new state until all input symbols have been consumed.Unlike a DFA, it is non-deterministic in that, for any input symbol, its next state may be any one of several possible states. Thus, in the formal definition, the next state is an element of the power set of states. This element, itself a set, represents some subset of all possible states to be considered at once.
The notion of accepting an input is similar to that for the DFA. When the last input symbol is consumed, the NFA accepts if and only if there is some set of transitions that will take it to an accepting state. Equivalently, it rejects, if, no matter what transitions are applied, it would not end in an accepting state.
An extension of the NFA is the NFA-ε (also known as NFA-λ or the NFA with epsilon moves), which allows a transformation to a new state without consuming any input symbols. Transformations to new states without consuming an input symbol are called ε-transitions or λ-transitions. They are usually labeled with the Greek letter ε or λ. For example, if it is in state 1, with the next input symbol an a, it can move to state 2 without consuming any input symbols, and thus there is an ambiguity: is the system in state 1, or state 2, before consuming the letter a? Because of this ambiguity, it is more convenient to talk of the set of possible states the system may be in. Thus, before consuming letter a, the NFA-epsilon may be in any one of the states out of the set {1,2}. Equivalently, one may imagine that the NFA is in state 1 and 2 'at the same time': and this gives an informal hint of the powerset construction
Powerset construction
In the theory of computation and Automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton into a deterministic finite automaton which recognizes the same formal language...
: the DFA equivalent to an NFA is defined as the one that is in the state q={1,2}.
Formal definition
An NFA is represented formally by a 5-tuple,(Q, Σ, Δ, q0, F), consisting of
- a finite set of states Q
- a finite set of input symbols Σ
- a transition functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
Δ : Q × Σ → P(Q). - an initial (or start) state q0 ∈ Q
- a set of states F distinguished as accepting (or final) states F ⊆ Q.
Here, P(Q) denotes the power set of Q.
Let w = a1a2 ... an be a word over the alphabet Σ. The automaton M accepts the word w if a sequence of states,
r0,r1, ..., rn, exists in Q with the following conditions:
- r0 = q0
- ri+1 ∈ Δ(ri, ai+1), for i = 0, ..., n−1
- rn ∈ F.
In words, the first condition says that the machine starts in the start state q0. The second condition says that given each character of string w, the machine will transition from state to state according to the transition relation Δ. The last condition says that the machine accepts w if the last input of w causes the machine to halt in one of the accepting states. Otherwise, it is said that the automaton rejects the string. The set of strings M accepts is the language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
recognized by M and this language is denoted by L(M).
For more comprehensive introduction of the formal definition see automata theory
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
.
NFA-ε
The NFA-ε (also sometimes called NFA-λ or NFA with epsilon moves) replaces the transition function with one that allows the empty string
Empty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
ε as a possible input, so that one has instead
- Δ : Q × (Σ ∪{ε}) → P(Q).
It can be shown that ordinary NFA and NFA-ε are equivalent, in that, given either one, one can construct the other, which recognizes the same language.
Example
In formal notation, let M = ({s0, s1, s2, s3, s4}, {0, 1}, Δ, s0, {s1, s3}) where
the transition relation T can be defined by this state transition table
State transition table
In automata theory and sequential logic, a state transition table is a table showing what state a finite semiautomaton or finite state machine will move to, based on the current state and other inputs...
:
M can be viewed as the union of two DFA
Deterministic finite state machine
In the theory of computation and automata theory, a deterministic finite state machine—also known as deterministic finite automaton —is a finite state machine accepting finite strings of symbols. For each state, there is a transition arrow leading out to a next state for each symbol...
s: one with states {S1, S2} and the other with states {S3, S4}.
The language of M can be described by the regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
given by this regular expression
Regular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
(1*(01*01*)*) ∪ (0*(10*10*)*).
We define M using ε-moves
but M can be defined without using ε-moves.
Properties
The machine starts in the specified initial state and reads in a string of symbols from its alphabet. The automaton uses the state transition function Δ to determine the next state using the current state, and the symbol just read or the empty string. However, "the next state of an NFA depends not only on the current input event, but also on an arbitrary number of subsequent input events. Until these subsequent events occur it is not possible to determine which state the machine is in". If, when the automaton has finished reading, it is in an accepting state, the NFA is said to accept the string, otherwise it is said to reject the string.The set of all strings accepted by an NFA is the language the NFA accepts. This language is a regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
.
For every NFA a deterministic finite state machine
Deterministic finite state machine
In the theory of computation and automata theory, a deterministic finite state machine—also known as deterministic finite automaton —is a finite state machine accepting finite strings of symbols. For each state, there is a transition arrow leading out to a next state for each symbol...
(DFA) can be found that accepts the same language. Therefore it is possible to convert an existing NFA into a DFA for the purpose of implementing a (perhaps) simpler machine. This can be performed using the powerset construction
Powerset construction
In the theory of computation and Automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton into a deterministic finite automaton which recognizes the same formal language...
, which may lead to an exponential rise in the number of necessary states. A formal proof of the powerset construction is given here.
Properties of NFA-ε
For all one writes if and only if can be reached from by going along zero or more arrows. In other words, if and only if there exists where such thatFor any
, the set of states that can be reached from p is called the epsilon-closure or ε-closure of p, and is written asFor any subset
, define the ε-closure of P asThe ε-transitions are transitive, in that it may be shown that, for all
and , if and , then .Similarly, if
and then Let x be a string over the alphabet Σ∪{ε}. An NFA-ε M accepts the string x if there exist both a representation of x of the form x1x2 ... xn, where xi ∈ (Σ ∪{ε}), and a sequence of states
p0,p1, ..., pn, where pi ∈ Q, meeting the following conditions:
- p0
E({q0}) - pi
E(T(pi−1, xi)) for i = 1, ..., n - pn ∈ F.
Implementation
There are many ways to implement a NFA:- Convert to the equivalent DFA. In some cases this may cause exponential blowup in the size of the automaton and thus auxiliary space proportional to the number of states in the NFA (as storage of the state value requires at most one bit for every state in the NFA)
- Keep a set data structure of all states which the machine might currently be in. On the consumption of the last input symbol, if one of these states is a final state, the machine accepts the string. In the worst case, this may require auxiliary space proportional to the number of states in the NFA; if the set structure uses one bit per NFA state, then this solution is exactly equivalent to the above.
- Create multiple copies. For each n way decision, the NFA creates up to
copies of the machine. Each will enter a separate state. If, upon consuming the last input symbol, at least one copy of the NFA is in the accepting state, the NFA will accept. (This, too, requires linear storage with respect to the number of NFA states, as there can be one machine for every NFA state.) - Explicitly propagate tokens through the transition structure of the NFA and match whenever a token reaches the final state. This is sometimes useful when the NFA should encode additional context about the events that triggered the transition. (For an implementation that uses this technique to keep track of object references have a look at Tracematches.)
Application of NFA-ε
NFAs and DFAs are equivalent in that if a language is recognized by an NFA, it is also recognized by a DFA and vice versa. The establishment of such equivalence is important and useful. It is useful because constructing an NFA to recognize a given language is sometimes much easier than constructing a DFA for that language. It is important because NFAs can be used to reduce the complexity of the mathematical work required to establish many important properties in the theory of computationTheory of computation
In theoretical computer science, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm...
. For example, it is much easier to prove the following properties using NFAs than DFAs:
- The unionUnion of two regular languagesIn formal language theory, and in particular the theory of nondeterministic finite state machines, it is known that the union of two regular languages is a regular language...
of two regular languageRegular languageIn theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s is regular. - The concatenation of two regular languageRegular languageIn theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s is regular. - The Kleene closure of a regular languageRegular languageIn theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
is regular.