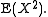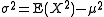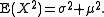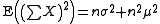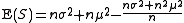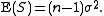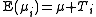Squared deviations
Encyclopedia
In probability theory
and statistics
, the definition of variance
is either the expected value
(when considering a theoretical distribution
), or average value (for actual experimental data), of squared deviations from the mean. Computations for analysis of variance
involve the partitioning of a sum of squared deviations. An understanding of the complex computations involved is greatly enhanced by a detailed study of the statistical value:
It is well-known that for a random variable
 with mean
with mean 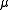 and variance
and variance  :
:
Therefore
From the above, the following are easily derived:
From the two derived expectations above the expected value of this sum is
which implies
This effectively proves the use of the divisor n − 1 in the calculation of an unbiased sample estimate of σ2.
and the variance of each treatment group is unchanged from the population variance .
.
Under the Null Hypothesis that the treatments have no effect, then each of the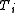 will be zero.
will be zero.
It is now possible to calculate three sums of squares:
Individual
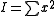
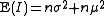
Treatments
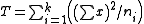
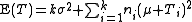

Under the null hypothesis that the treatments cause no differences and all the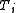 are zero, the expectation simplifies to
are zero, the expectation simplifies to
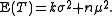
Combination
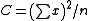
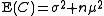
 , only
, only  .
.
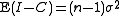 total squared deviations
total squared deviations
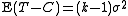 treatment squared deviations
treatment squared deviations
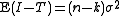 residual squared deviations
residual squared deviations
The constants (n − 1), (k − 1), and (n − k) are normally referred to as the number of degrees of freedom
.
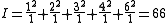
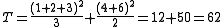

Giving
Five sums of squares are calculated:
Finally, the sums of squared deviations required for the analysis of variance
can be calculated.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the definition of variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is either the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
(when considering a theoretical distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
), or average value (for actual experimental data), of squared deviations from the mean. Computations for analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
involve the partitioning of a sum of squared deviations. An understanding of the complex computations involved is greatly enhanced by a detailed study of the statistical value:
It is well-known that for a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
 with mean
with mean 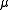 and variance
and variance  :
:Therefore
From the above, the following are easily derived:
Sample variance
The sum of squared deviations needed to calculate variance (before deciding whether to divide by n or n − 1) is most easily calculated asFrom the two derived expectations above the expected value of this sum is
which implies
This effectively proves the use of the divisor n − 1 in the calculation of an unbiased sample estimate of σ2.
Partition — analysis of variance
In the situation where data is available for k different treatment groups having size ni where i varies from 1 to k, then it is assumed that the expected mean of each group isand the variance of each treatment group is unchanged from the population variance
 .
.Under the Null Hypothesis that the treatments have no effect, then each of the
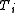 will be zero.
will be zero.It is now possible to calculate three sums of squares:
Individual
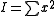
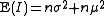
Treatments
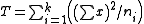
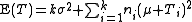

Under the null hypothesis that the treatments cause no differences and all the
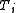 are zero, the expectation simplifies to
are zero, the expectation simplifies to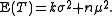
Combination
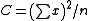
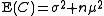
Sums of squared deviations
Under the null hypothesis, the difference of any pair of I, T, and C does not contain any dependency on , only
, only  .
.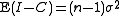 total squared deviations
total squared deviations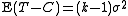 treatment squared deviations
treatment squared deviations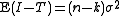 residual squared deviations
residual squared deviationsThe constants (n − 1), (k − 1), and (n − k) are normally referred to as the number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
.
Example
In a very simple example, 5 observations arise from two treatments. The first treatment gives three values 1, 2, and 3, and the second treatment gives two values 4, and 6.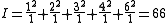
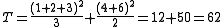

Giving
- Total squared deviations = 66 − 51.2 = 14.8 with 4 degrees of freedom.
- Treatment squared deviations = 62 − 51.2 = 10.8 with 1 degree of freedom.
- Residual squared deviations = 66 − 62 = 4 with 3 degrees of freedom.
Two-way analysis of variance
The following hypothetical example gives the yields of 15 plants subject to two different environmental variations, and three different fertilisers.| Extra CO2 | Extra humidity | |
|---|---|---|
| No fertiliser | 7, 2, 1 | 7, 6 |
| Nitrate | 11, 6 | 10, 7, 3 |
| Phosphate | 5, 3, 4 | 11, 4 |
Five sums of squares are calculated:
| Factor | Calculation | Sum |  |
|---|---|---|---|
| Individual | 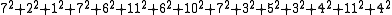 |
641 | 15 |
| Fertiliser × Environment | 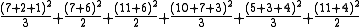 |
556.1667 | 6 |
| Fertiliser |  |
525.4 | 3 |
| Environment | 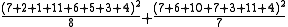 |
519.2679 | 2 |
| Composite | 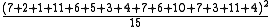 |
504.6 | 1 |
Finally, the sums of squared deviations required for the analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
can be calculated.
| Factor | Sum | 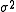 |
Total | Environment | Fertiliser | Fertiliser × Environment | Residual |
|---|---|---|---|---|---|---|---|
| Individual | 641 | 15 | 1 | 1 | |||
| Fertiliser × Environment | 556.1667 | 6 | 1 | −1 | |||
| Fertiliser | 525.4 | 3 | 1 | −1 | |||
| Environment | 519.2679 | 2 | 1 | −1 | |||
| Composite | 504.6 | 1 | −1 | −1 | −1 | 1 | |
| Squared deviations | 136.4 | 14.668 | 20.8 | 16.099 | 84.833 | ||
| Degrees of freedom | 14 | 1 | 2 | 2 | 9 |