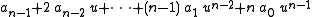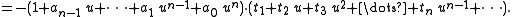Splitting circle method
Encyclopedia
In mathematics
, the splitting circle method is a numerical algorithm
for the numerical factorization of a polynomial
and, ultimately, for finding its complex
roots. It was introduced by Arnold Schönhage
in his 1982 paper The fundamental theorem of algebra in terms of computational complexity (Technical report, Mathematisches Institut der Universität Tübingen). A revised algorithm was presented by Victor Pan
in 1998. An implementation was provided by Xavier Gourdon in 1996 for the Magma
and PARI/GP
computer algebra systems.
, more precisely the residue theorem
, to construct factors of polynomials. With those methods it is possible to construct a factor of a given polynomial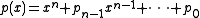
for any region of the complex plane with a piecewise smooth boundary. Most of those factors will be trivial, that is constant polynomials. Only regions that contain roots of p(x) result in nontrivial factors that have exactly those roots of p(x) as their own roots, preserving multiplicity.
In the numerical realization of this method one uses disks D(c,r) (center c, radius r) in the complex plane as regions. The boundary circle of a disk splits the set of roots of p(x) in two parts, hence the name of the method. To a given disk one computes approximate factors following the analytical theory and refines them using Newton's method
. To avoid numerical instability one has to demand that all roots are well separated from the boundary circle of the disk. So to obtain a good splitting circle it should be embedded in a root free annulus A(c,r,R) (center c, inner radius r, outer radius R) with a large relative width R/r.
Repeating this process for the factors found, one finally arrives at an approximative factorization of the polynomial at a required precision. The factors are either linear polynomials representing well isolated zeros or higher order polynomials representing clusters of zeros.
are a bijective relation between the elementary symmetric polynomial
s of a tuple of complex numbers and its sums of powers. Therefore, it is possible to compute the coefficients of a polynomial
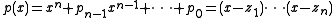
(or of a factor of it) from the sums of powers of its zeros
, 
by solving the triangular system that is obtained by comparing the powers of u in the following identity of formal power series
If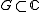
is a domain with piecewise smooth boundary C and if the zeros of p(x) are pairwise distinct and not on the boundary C, then from the residue theorem
of residual calculus one gets
The identity of the left to the right side of this equation also holds for zeros with multiplicities. By using the Newton identities one is able to compute from those sums of powers the factor
of p(x) corresponding to the zeros of p(x) inside G. By polynomial division one also obtains the second factor g(x) in p(x) = f(x)g(x).
The commonly used regions are circles in the complex plane. Each circle gives raise to a split of the polynomial p(x) in factors f(x) and g(x). Repeating this procedure on the factors using different circles yields finer and finer factorizations. This recursion stops after a finite number of proper splits with all factors being nontrivial powers of linear polynomials.
The challenge now consists in the conversion of this analytical procedure into a numerical algorithm with good running time. The integration is approximated by a finite sum of a numerical integration method, making use of the fast Fourier transform
for the evaluation of the polynomials p(x) and p' (x). The polynomial f(x) that results will only be an approximate factor. To ensure that its zeros are close to the zeros of p inside G and only to those, one must demand that all zeros of p are far away from the boundary C of the region G.
be a polynomial of degree n has k zeros inside the circle of radius 1/2 and the remaining n-k zeros outside the circle of radius 2. With N=O(k) large enough, the approximation of the contour integrals using N points results in an approximation 
of the factor f with error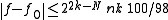
,
where the norm of a polynomial is the sum of the moduli of its coefficients.
Since the zeros of a polynomial are continuous in its coefficients, one can make the zeros of
as close as wanted to the zeros of f by choosing N large enough. However, one can improve this approximation faster using a Newton method. Division of p with remainder yields an approximation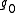 
of the remaining factor g. Now
,
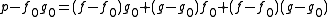so discarding the last second order term one has to solve
using any variant of the extended euclidian algorithm to obtain the incremented approximations 
and 
. This is repeated until the increments are zero relative to the chosen precision.
To remedy this situation, the Graeffe iteration is applied. It computes a sequence of polynomials
where the roots of
are the 
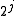-th dyadic powers of the roots of the initial polynomial p. By splitting 
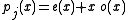into even and odd parts, the succeeding polynomial is obtained by purely arithmetic operations as 
. The ratios of the absolute moduli of the roots increase by the same power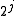 
and thus tend to infinity. Choosing j large enough one finally finds a splitting annulus of relative width 4 around the origin.
The approximate factorization of
is now to be lifted back to the original polynomial. To this end an alternation of Newton steps and Pade approximation
s is used. It is easy to check that
holds. The polynomials on the left side are known in step j, the polynomials on the right side can bo obtained as Padé approximant
s of the corresponding degrees for the power series expansion of the fraction on the left side.
of any root of p(x) to any of the five center points 0, 2R, −2R, 2Ri, −2Ri and selects the one with the largest ratio 
between the two. By this construction it can be guaranteed that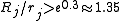 
for at least one center. For such a center there has to be a root-free annulus of relative width 
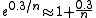. After 
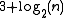Graeffe iterations, the corresponding annulus of the iterated polynomial has a relative width greater than 11 > 4, as required for the initial splitting described above (see Schönhage (1982)). After 
Graeffe iterations, the corresponding annulus has a relative width greater than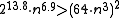 
, allowing a much simplified initial splitting (see Malajovich/Zubelli (1997))
To locate the best root-free annulus one uses a consequence of the Rouché theorem: For k = 1, ..., n − 1 the polynomial equation
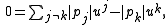
u > 0, has, by Descartes' rule of signs
zero or two positive roots
. In the latter case, there are exactly k roots inside the (closed) disk 
and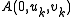 
is a root-free (open) annulus.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the splitting circle method is a numerical algorithm
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
for the numerical factorization of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
and, ultimately, for finding its complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
roots. It was introduced by Arnold Schönhage
Arnold Schönhage
Arnold Schönhage is a mathematician and computer scientist and Professor Emeritus at Rheinische Friedrich-Wilhelms-Universität, Bonn. He was also professor in Tübingen and Konstanz...
in his 1982 paper The fundamental theorem of algebra in terms of computational complexity (Technical report, Mathematisches Institut der Universität Tübingen). A revised algorithm was presented by Victor Pan
Victor Pan
Victor Ya. Pan is a Soviet and American mathematician and computer scientist. He earned his Ph.D. at Moscow University then continued at the Soviet Academy of Sciences. During that time, he published a number of significant papers and became known informally as "polynomial Pan" for his pioneering...
in 1998. An implementation was provided by Xavier Gourdon in 1996 for the Magma
Magma computer algebra system
Magma is a computer algebra system designed to solve problems in algebra, number theory, geometry and combinatorics. It is named after the algebraic structure magma...
and PARI/GP
PARI/GP
PARI/GP is a computer algebra system with the main aim of facilitating number theory computations. It is free software; versions 2.1.0 and higher are distributed under the GNU General Public License...
computer algebra systems.
General description
The fundamental idea of the splitting circle method is to use methods of complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, more precisely the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
, to construct factors of polynomials. With those methods it is possible to construct a factor of a given polynomial
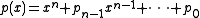for any region of the complex plane with a piecewise smooth boundary. Most of those factors will be trivial, that is constant polynomials. Only regions that contain roots of p(x) result in nontrivial factors that have exactly those roots of p(x) as their own roots, preserving multiplicity.In the numerical realization of this method one uses disks D(c,r) (center c, radius r) in the complex plane as regions. The boundary circle of a disk splits the set of roots of p(x) in two parts, hence the name of the method. To a given disk one computes approximate factors following the analytical theory and refines them using Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. To avoid numerical instability one has to demand that all roots are well separated from the boundary circle of the disk. So to obtain a good splitting circle it should be embedded in a root free annulus A(c,r,R) (center c, inner radius r, outer radius R) with a large relative width R/r.
Repeating this process for the factors found, one finally arrives at an approximative factorization of the polynomial at a required precision. The factors are either linear polynomials representing well isolated zeros or higher order polynomials representing clusters of zeros.
Details of the analytical construction
The Newton's identitiesNewton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
are a bijective relation between the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s of a tuple of complex numbers and its sums of powers. Therefore, it is possible to compute the coefficients of a polynomial
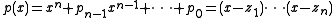
(or of a factor of it) from the sums of powers of its zeros
, by solving the triangular system that is obtained by comparing the powers of u in the following identity of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
If
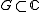is a domain with piecewise smooth boundary C and if the zeros of p(x) are pairwise distinct and not on the boundary C, then from the residue theoremResidue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
of residual calculus one gets
The identity of the left to the right side of this equation also holds for zeros with multiplicities. By using the Newton identities one is able to compute from those sums of powers the factor
of p(x) corresponding to the zeros of p(x) inside G. By polynomial division one also obtains the second factor g(x) in p(x) = f(x)g(x).
The commonly used regions are circles in the complex plane. Each circle gives raise to a split of the polynomial p(x) in factors f(x) and g(x). Repeating this procedure on the factors using different circles yields finer and finer factorizations. This recursion stops after a finite number of proper splits with all factors being nontrivial powers of linear polynomials.
The challenge now consists in the conversion of this analytical procedure into a numerical algorithm with good running time. The integration is approximated by a finite sum of a numerical integration method, making use of the fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
for the evaluation of the polynomials p(x) and p
Basic numerical observation
(Schönhage 1982) Let be a polynomial of degree n has k zeros inside the circle of radius 1/2 and the remaining n-k zeros outside the circle of radius 2. With N=O(k) large enough, the approximation of the contour integrals using N points results in an approximation of the factor f with error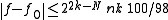,where the norm of a polynomial is the sum of the moduli of its coefficients.
Since the zeros of a polynomial are continuous in its coefficients, one can make the zeros of
as close as wanted to the zeros of f by choosing N large enough. However, one can improve this approximation faster using a Newton method. Division of p with remainder yields an approximation 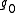of the remaining factor g. Now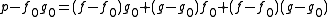,so discarding the last second order term one has to solve
using any variant of the extended euclidian algorithm to obtain the incremented approximations and . This is repeated until the increments are zero relative to the chosen precision.Graeffe iteration
The crucial step in this method is to find an annulus of relative width 4 in the complex plane that contains no zeros of p and contains approximately as many zeros of p inside as outside of it. Any annulus of this characteristic can be transformed, by translation and scaling of the polynomial, into the annulus between the radii 1/2 and 2 around the origin. But, not every polynomial admits such a splitting annulus.To remedy this situation, the Graeffe iteration is applied. It computes a sequence of polynomials
where the roots of
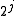are the -th dyadic powers of the roots of the initial polynomial p. By splitting 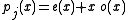into even and odd parts, the succeeding polynomial is obtained by purely arithmetic operations as . The ratios of the absolute moduli of the roots increase by the same power 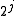and thus tend to infinity. Choosing j large enough one finally finds a splitting annulus of relative width 4 around the origin.The approximate factorization of
is now to be lifted back to the original polynomial. To this end an alternation of Newton steps and Pade approximationPadé approximant
Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....
s is used. It is easy to check that
holds. The polynomials on the left side are known in step j, the polynomials on the right side can bo obtained as Padé approximant
Padé approximant
Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....
s of the corresponding degrees for the power series expansion of the fraction on the left side.
Finding a good circle
Making use of the Graeffe iteration and any known estimate for the absolute value of the largest root one can find estimates R of this absolute value of any precision. Now one computes estimates for the largest and smallest distances of any root of p(x) to any of the five center points 0, 2R, −2R, 2Ri, −2Ri and selects the one with the largest ratio between the two. By this construction it can be guaranteed that 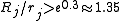for at least one center. For such a center there has to be a root-free annulus of relative width 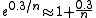. After 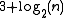Graeffe iterations, the corresponding annulus of the iterated polynomial has a relative width greater than 11 > 4, as required for the initial splitting described above (see Schönhage (1982)). After Graeffe iterations, the corresponding annulus has a relative width greater than 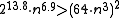, allowing a much simplified initial splitting (see Malajovich/Zubelli (1997))To locate the best root-free annulus one uses a consequence of the Rouché theorem: For k = 1, ..., n − 1 the polynomial equation
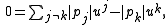
u > 0, has, by Descartes' rule of signs
Descartes' rule of signs
In mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial....
zero or two positive roots
. In the latter case, there are exactly k roots inside the (closed) disk and 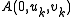is a root-free (open) annulus.