Spectral asymmetry
Encyclopedia
In mathematics
and physics
, the spectral asymmetry is the asymmetry in the distribution of the spectrum
of eigenvalues of an operator. In mathematics, the spectral asymmetry arises in the study of elliptic operator
s on compact manifolds, and is given a deep meaning by the Atiyah-Singer index theorem. In physics, it has numerous applications, typically resulting in a fractional charge
due to the asymmetry of the spectrum of a Dirac operator
. For example, the vacuum expectation value
of the baryon number is given by the spectral asymmetry of the Hamiltonian operator. The spectral asymmetry of the confined quark fields is an important property of the chiral bag model.
, an equal number of which are positive and negative, the spectral asymmetry may be defined as the sum
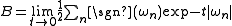
where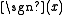
is the sign function
. Other regulator
s, such as the zeta function regulator, may be used.
The need for both a positive and negative spectrum in the definition is why the spectral asymmetry usually occurs in the study of Dirac operator
s.
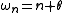
where n is an integer, ranging over all positive and negative values. One may show in a straightforward manner that the spectral asymmetry in this case is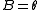
.
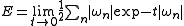
This sum is formally divergent, and the divergences must be accounted for and removed using standard regularization techniques.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the spectral asymmetry is the asymmetry in the distribution of the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of eigenvalues of an operator. In mathematics, the spectral asymmetry arises in the study of elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
s on compact manifolds, and is given a deep meaning by the Atiyah-Singer index theorem. In physics, it has numerous applications, typically resulting in a fractional charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
due to the asymmetry of the spectrum of a Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
. For example, the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the baryon number is given by the spectral asymmetry of the Hamiltonian operator. The spectral asymmetry of the confined quark fields is an important property of the chiral bag model.
Definition
Given an operator with eigenvalues, an equal number of which are positive and negative, the spectral asymmetry may be defined as the sum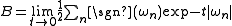where
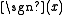is the sign functionSign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
. Other regulator
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
s, such as the zeta function regulator, may be used.
The need for both a positive and negative spectrum in the definition is why the spectral asymmetry usually occurs in the study of Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
s.
Example
As an example, consider an operator with a spectrum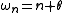where n is an integer, ranging over all positive and negative values. One may show in a straightforward manner that the spectral asymmetry in this case is
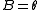.Discussion
Related to the spectral asymmetry is the vacuum expectation value of the energy associated with the operator, the Casimir energy, which is given by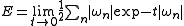This sum is formally divergent, and the divergences must be accounted for and removed using standard regularization techniques.