
Span (category theory)
Encyclopedia
A span, in category theory
, is a generalization of the notion of relation
between two objects of a category. When the category has all pullbacks
(and satisfies a small number of other conditions), spans can be considered as morphisms in a category of fractions
.
of type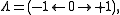 i.e., a diagram of the form
i.e., a diagram of the form 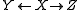 .
.
That is, let Λ be the category (-1 ← 0 → +1). Then a span in a category
C is a functor
S:Λ → C. This means that a span consists of three objects X, Y and Z of C and morphisms f:X → Y and g:X → Z: it is two maps with common domain.
The colimit of a span is a pushout
.
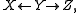
where the left morphism is in W, can be considered a generalised morphism (i.e., where one "inverts the weak equivalences"). Note that this is not the usual point of view taken when dealing with model categories.
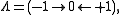 i.e., a diagram of the form
i.e., a diagram of the form  .
.
Thus it consists of three objects X, Y and Z of C and morphisms f:Y → X and g:Z → X: it is two maps with common codomain.
The limit
of a cospan is a pullback
.
An example of a cospan is a cobordism
W between two manifolds M and N, where the two maps are the inclusions into W. Note that while cobordisms are cospans, the category of cobordisms is not a "cospan category": it is not the category of all cospans in "the category of manifolds with inclusions on the boundary", but rather a subcategory thereof, as the requirement that M and N form a partition of the boundary of W is a global constraint.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, is a generalization of the notion of relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
between two objects of a category. When the category has all pullbacks
Pullback (category theory)
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
(and satisfies a small number of other conditions), spans can be considered as morphisms in a category of fractions
Localization of a category
In mathematics, localization of a category consists of adding to a category inverse morphisms for some collection of morphisms, constraining them to become isomorphisms. This is formally similar to the process of localization of a ring; it in general makes objects isomorphic that were not so before...
.
Formal definition
A span is a diagramDiagram (category theory)
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
of type
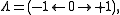 i.e., a diagram of the form
i.e., a diagram of the form 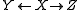 .
.That is, let Λ be the category (-1 ← 0 → +1). Then a span in a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
S:Λ → C. This means that a span consists of three objects X, Y and Z of C and morphisms f:X → Y and g:X → Z: it is two maps with common domain.
The colimit of a span is a pushout
Pushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
.
Examples
- If R is a relation between sets X and Y (i.e. a subset of X × Y), then X ← R → Y is a span, where the maps are the projection maps
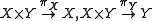 .
. - Any object yields the trivial span
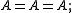 formally, the diagram A ← A → A, where the maps are the identity.
formally, the diagram A ← A → A, where the maps are the identity. - More generally, let
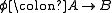 be a morphism in some category. There is a trivial span A = A → B; formally, the diagram A ← A → B, where the left map is the identity on A, and the right map is the given map φ.
be a morphism in some category. There is a trivial span A = A → B; formally, the diagram A ← A → B, where the left map is the identity on A, and the right map is the given map φ. - If M is a model categoryModel categoryIn mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
, with W the set of weak equivalenceWeak equivalence-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
s, then the spans of the form
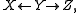
where the left morphism is in W, can be considered a generalised morphism (i.e., where one "inverts the weak equivalences"). Note that this is not the usual point of view taken when dealing with model categories.
Cospans
A cospan K in a category C is a functor K:Λop → C; equivalently, a contravariant functor from Λ to C. That is, a diagram of type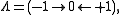 i.e., a diagram of the form
i.e., a diagram of the form  .
.Thus it consists of three objects X, Y and Z of C and morphisms f:Y → X and g:Z → X: it is two maps with common codomain.
The limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of a cospan is a pullback
Pullback (category theory)
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
.
An example of a cospan is a cobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
W between two manifolds M and N, where the two maps are the inclusions into W. Note that while cobordisms are cospans, the category of cobordisms is not a "cospan category": it is not the category of all cospans in "the category of manifolds with inclusions on the boundary", but rather a subcategory thereof, as the requirement that M and N form a partition of the boundary of W is a global constraint.
See also
- Binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
- Pullback (category theory)Pullback (category theory)In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
- Pushout (category theory)Pushout (category theory)In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
- CobordismCobordismIn mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...

