Slide attack
Encyclopedia
The slide attack is a form of cryptanalysis
designed to deal with the prevailing idea that even weak cipher
s can become very strong by increasing the number of rounds, which can ward off a differential attack. The slide attack works in such a way as to make the number of rounds in a cipher irrelevant. Rather than looking at the data-randomizing aspects of the block cipher, the slide attack works by analyzing the key schedule
and exploiting weaknesses in it to break the cipher. The most common one is the keys repeating in a cyclic manner.
The attack was first described by David Wagner and Alex Biryukov
. Bruce Schneier
first suggested the term slide attack to them, and they used it in their 1999 paper describing the attack.
The only requirements for a slide attack to work on a cipher is that it can be broken down into multiple rounds of an identical F function. This probably means that it has a cyclic key schedule. The F function must be vulnerable to a known-plaintext attack
. The slide attack is closely related to the related-key attack
.
The idea of the slide attack has roots in a paper published by Edna Grossman
and Bryant Tuckerman
in an IBM Technical Report in 1977. Grossman and Tuckerman demonstrated the attack on a weak block cipher
named New Data Seal
(NDS). The attack relied on the fact that the cipher has identical subkeys in each round, so the cipher had a cyclic key schedule with a cycle of only one key, which makes it an early version of the slide attack. A summary of the report, including a description of the NDS block cipher and the attack, is given in Cipher Systems (Beker & Piper, 1982).
as keys of any length.
The slide attack works by breaking the cipher up into identical permutation
functions, F. This F function may consist of more than one round
of the cipher; it is defined by the key-schedule. For example, if a cipher uses an alternating key schedule where it switches between a
and 
for each round, the F function would consist of two rounds. Each of the 
will
appear at least once in F.
The next step is to collect
plaintext-ciphertext pairs. Depending on
the characteristics of the cipher fewer may suffice, but by the birthday paradox
no more than
should be needed. These pairs, which denoted as 
are then used to find a slid pair which denoted 
. A slid pair has the property that 
and that 
. Once a slid pair is identified, the cipher is broken because of the vulnerability to known-plaintext attacks. The key can easily be extracted from this pairing.
The slid pair can be thought to be what happens to a message after one application of the function F. It is ’slid’ over one encryption round and this is where the attack gets its
name.
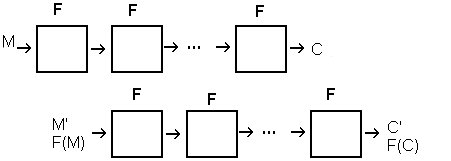
The process of finding a slid pair is somewhat different for each cipher
but follows the same basic scheme. One uses the fact that it is relatively
easy to extract the key from just one iteration of F. Choose any pair of
plaintext-ciphertext pairs,
and check to see what the keys corresponding to 
and 
are. If these keys match, this is a slid pair; otherwise move on to the next pair.
With
plaintext-ciphertext pairs one slid pair is expected, along with a small number of false-positives depending on the structure of the cipher. The false positives
can be eliminated by using the keys on a different message-ciphertext pair to see if the encryption is correct. The probability that the wrong key will correctly encipher two or more messages is very low for a good cipher.
Sometimes the structure of the cipher greatly reduces the number of
plaintext-ciphertext pairs needed, and thus also a large amount of the work.
The clearest of these examples is the Feistel cipher
using a cyclic key schedule.
The reason for this is given a
the search is for a 
. This reduces the possible paired messages from 
down to
(since half the message is fixed) and so at most 
plaintext-ciphertext pairs are needed in order to find a slid-pair.
Cryptanalysis
Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
designed to deal with the prevailing idea that even weak cipher
Cipher
In cryptography, a cipher is an algorithm for performing encryption or decryption — a series of well-defined steps that can be followed as a procedure. An alternative, less common term is encipherment. In non-technical usage, a “cipher” is the same thing as a “code”; however, the concepts...
s can become very strong by increasing the number of rounds, which can ward off a differential attack. The slide attack works in such a way as to make the number of rounds in a cipher irrelevant. Rather than looking at the data-randomizing aspects of the block cipher, the slide attack works by analyzing the key schedule
Key schedule
[[Image:DES-key-schedule.png|thumbnail|220px|The key schedule of DES [[Image:DES-key-schedule.png|thumbnail|220px|The key schedule of DES [[Image:DES-key-schedule.png|thumbnail|220px|The key schedule of DES ("[[Image:DES-key-schedule.png|thumbnail|220px|The key schedule of DES ("...
and exploiting weaknesses in it to break the cipher. The most common one is the keys repeating in a cyclic manner.
The attack was first described by David Wagner and Alex Biryukov
Alex Biryukov
Alex Biryukov is a cryptographer, currently an assistant professor at the University of Luxembourg. His notable work includes the design of the stream cipher LEX, as well as the cryptanalysis of numerous cryptographic primitives. In 1998, he developed impossible differential cryptanalysis together...
. Bruce Schneier
Bruce Schneier
Bruce Schneier is an American cryptographer, computer security specialist, and writer. He is the author of several books on general security topics, computer security and cryptography, and is the founder and chief technology officer of BT Managed Security Solutions, formerly Counterpane Internet...
first suggested the term slide attack to them, and they used it in their 1999 paper describing the attack.
The only requirements for a slide attack to work on a cipher is that it can be broken down into multiple rounds of an identical F function. This probably means that it has a cyclic key schedule. The F function must be vulnerable to a known-plaintext attack
Known-plaintext attack
The known-plaintext attack is an attack model for cryptanalysis where the attacker has samples of both the plaintext , and its encrypted version . These can be used to reveal further secret information such as secret keys and code books...
. The slide attack is closely related to the related-key attack
Related-key attack
In cryptography, a related-key attack is any form of cryptanalysis where the attacker can observe the operation of a cipher under several different keys whose values are initially unknown, but where some mathematical relationship connecting the keys is known to the attacker...
.
The idea of the slide attack has roots in a paper published by Edna Grossman
Edna Grossman
Edna Grossman is an American mathematician. She was born in Germany, grew up in Brooklyn, New York, and graduated with a B.S. in mathematics from Brooklyn College. She earned her M.S. in mathematics from New York University's Courant Institute of Mathematical Sciences, where she also received her...
and Bryant Tuckerman
Bryant Tuckerman
Louis Bryant Tuckerman, III was an American mathematician, born in Lincoln, Nebraska. He was a member of the team that developed the Data Encryption Standard ....
in an IBM Technical Report in 1977. Grossman and Tuckerman demonstrated the attack on a weak block cipher
Block cipher
In cryptography, a block cipher is a symmetric key cipher operating on fixed-length groups of bits, called blocks, with an unvarying transformation. A block cipher encryption algorithm might take a 128-bit block of plaintext as input, and output a corresponding 128-bit block of ciphertext...
named New Data Seal
New Data Seal
In cryptography, New Data Seal is a block cipher that was designed at IBM in 1975, based on the Lucifer algorithm that became DES.The cipher uses a block size of 128 bits, and a very large key size of 2048 bits. Like DES it has a 16-round Feistel network structure. The round function uses two...
(NDS). The attack relied on the fact that the cipher has identical subkeys in each round, so the cipher had a cyclic key schedule with a cycle of only one key, which makes it an early version of the slide attack. A summary of the report, including a description of the NDS block cipher and the attack, is given in Cipher Systems (Beker & Piper, 1982).
The actual attack
First, to introduce some notation. In this section assume the cipher takes n bit blocks and has a key-schedule using as keys of any length.The slide attack works by breaking the cipher up into identical permutation
functions, F. This F function may consist of more than one round
of the cipher; it is defined by the key-schedule. For example, if a cipher uses an alternating key schedule where it switches between a
and for each round, the F function would consist of two rounds. Each of the willappear at least once in F.
The next step is to collect
plaintext-ciphertext pairs. Depending onthe characteristics of the cipher fewer may suffice, but by the birthday paradox
Birthday paradox
In probability theory, the birthday problem or birthday paradox pertains to the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 366. However, 99%...
no more than
should be needed. These pairs, which denoted as are then used to find a slid pair which denoted . A slid pair has the property that and that . Once a slid pair is identified, the cipher is broken because of the vulnerability to known-plaintext attacks. The key can easily be extracted from this pairing.The slid pair can be thought to be what happens to a message after one application of the function F. It is ’slid’ over one encryption round and this is where the attack gets its
name.
The process of finding a slid pair is somewhat different for each cipher
but follows the same basic scheme. One uses the fact that it is relatively
easy to extract the key from just one iteration of F. Choose any pair of
plaintext-ciphertext pairs,
and check to see what the keys corresponding to and are. If these keys match, this is a slid pair; otherwise move on to the next pair.With
plaintext-ciphertext pairs one slid pair is expected, along with a small number of false-positives depending on the structure of the cipher. The false positivescan be eliminated by using the keys on a different message-ciphertext pair to see if the encryption is correct. The probability that the wrong key will correctly encipher two or more messages is very low for a good cipher.
Sometimes the structure of the cipher greatly reduces the number of
plaintext-ciphertext pairs needed, and thus also a large amount of the work.
The clearest of these examples is the Feistel cipher
Feistel cipher
In cryptography, a Feistel cipher is a symmetric structure used in the construction of block ciphers, named after the German-born physicist and cryptographer Horst Feistel who did pioneering research while working for IBM ; it is also commonly known as a Feistel network. A large proportion of block...
using a cyclic key schedule.
The reason for this is given a
the search is for a . This reduces the possible paired messages from down to
(since half the message is fixed) and so at most plaintext-ciphertext pairs are needed in order to find a slid-pair.