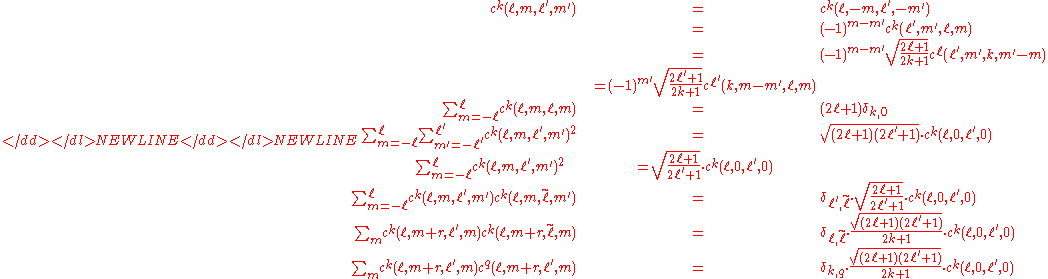Slater integrals
Encyclopedia
In mathematics and mathematical physics, Slater integrals are certain integrals of products of three spherical harmonic
s. They occur naturally when applying an orthonormal basis
of functions on the unit sphere
that transform in a particular way under rotations in three dimensions. Such integrals are particularly useful when computing properties of atoms which have natural spherical symmetry. These integrals are defined below along with some of their mathematical properties.
of atomic structure, John C. Slater
defined the integral of three spherical harmonics as a coefficient . These coefficients can be related to the Wigner 3jm symbols.
. These coefficients can be related to the Wigner 3jm symbols.
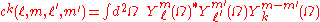
These integrals are useful and necessary when doing atomic calculations of the Hartree–Fock variety where matrix elements of the Coulomb operator
and Exchange operator
are needed. For an explicit formula, one can use Gaunt's formula for associated Legendre polynomials
.
Note that the product of two spherical harmonics can be written in terms of these coefficients. By expanding such a product over a spherical harmonic
basis
one may then multiply by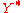 and integrate, using the conjugate property and being careful with phases and normalisations:
and integrate, using the conjugate property and being careful with phases and normalisations: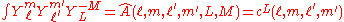
These coefficient obey a number of identities. They include
Spherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s. They occur naturally when applying an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of functions on the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
that transform in a particular way under rotations in three dimensions. Such integrals are particularly useful when computing properties of atoms which have natural spherical symmetry. These integrals are defined below along with some of their mathematical properties.
Formulation
In connection with the quantum theoryQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
of atomic structure, John C. Slater
John C. Slater
John Clarke Slater was a noted American physicist who made major contributions to the theory of the electronic structure of atoms, molecules and solids. This work is of ongoing importance in chemistry, as well as in many areas of physics. He also made major contributions to microwave electronics....
defined the integral of three spherical harmonics as a coefficient
 . These coefficients can be related to the Wigner 3jm symbols.
. These coefficients can be related to the Wigner 3jm symbols.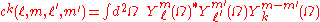
These integrals are useful and necessary when doing atomic calculations of the Hartree–Fock variety where matrix elements of the Coulomb operator
Coulomb operator
The Coulomb operator, named after Charles-Augustin de Coulomb, is a quantum mechanical operator used in the field of quantum chemistry. Specifically, it is a term found in the Fock operator...
and Exchange operator
Exchange operator
The Exchange operator is a quantum mechanical operator used in the field of quantum chemistry. Specifically, it is a term found in the Fock operator...
are needed. For an explicit formula, one can use Gaunt's formula for associated Legendre polynomials
Associated Legendre polynomials
In mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
.
Note that the product of two spherical harmonics can be written in terms of these coefficients. By expanding such a product over a spherical harmonic
Spherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
basis

one may then multiply by
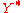 and integrate, using the conjugate property and being careful with phases and normalisations:
and integrate, using the conjugate property and being careful with phases and normalisations: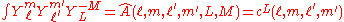
These coefficient obey a number of identities. They include