Similarities between Wiener and LMS
Encyclopedia
The Least mean squares filter
solution converges to the Wiener filter
solution, assuming that the unknown system is LTI
and the noise is stationary
. Both filters can be used to identify the impulse response of an unknown system, knowing only the original input signal and the output of the unknown system. By relaxing the error criterion to reduce current sample error instead of minimizing the total error over all of n, the LMS algorithm can be derived from the Wiener filter.
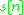, the output of an unknown LTI system 
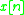can be expressed as:
where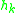
is an unknown filter tap coefficients and 
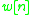is noise.
The model system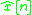
, using a Wiener filter solution with an order N, can be expressed as:
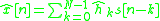
where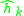
are the filter tap coefficients to be determined.
The error between the model and the unknown system can be expressed as:
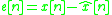
The total error
can be expressed as:
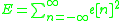
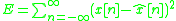
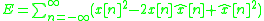
Use the Minimum mean-square error
criterion over all of
by setting its gradient
to zero:
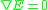
which is
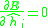
for all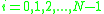
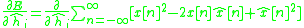
Substitute the definition of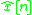
:
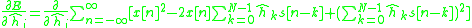
Distribute the partial derivative:
Using the definition of discrete cross-correlation
:
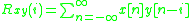
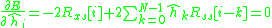
Rearrange the terms:
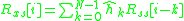
for all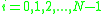
This system of N equations with N unknowns can be determined.
, the LMS algorithm can be derived.
The squared error can be expressed as:
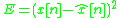
Using the Minimum mean-square error
criterion, take the gradient:
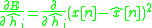
Apply chain rule and substitute definition of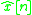
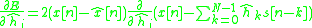
From this equation, we can derive an update equation for each
at every new 
using gradient descent
and a step size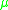
:
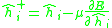
which becomes, for i = 0, 1, ..., N-1,
This is the LMS update equation.
Least mean squares filter
Least mean squares algorithms are a class of adaptive filter used to mimic a desired filter by finding the filter coefficients that relate to producing the least mean squares of the error signal . It is a stochastic gradient descent method in that the filter is only adapted based on the error at...
solution converges to the Wiener filter
Wiener filter
In signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
solution, assuming that the unknown system is LTI
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
and the noise is stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
. Both filters can be used to identify the impulse response of an unknown system, knowing only the original input signal and the output of the unknown system. By relaxing the error criterion to reduce current sample error instead of minimizing the total error over all of n, the LMS algorithm can be derived from the Wiener filter.
Derivation of the Wiener filter for system identification
Given a known input signal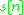, the output of an unknown LTI system 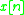can be expressed as:where
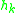is an unknown filter tap coefficients and 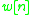is noise.The model system
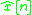, using a Wiener filter solution with an order N, can be expressed as: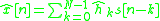where
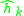are the filter tap coefficients to be determined.The error between the model and the unknown system can be expressed as:
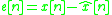
The total error
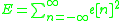
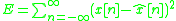
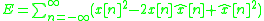
can be expressed as:Use the Minimum mean-square error
Minimum mean-square error
In statistics and signal processing, a minimum mean square error estimator describes the approach which minimizes the mean square error , which is a common measure of estimator quality....
criterion over all of
by setting its gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
to zero:
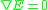
which is
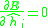
for all
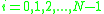
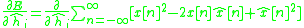
Substitute the definition of
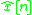:Distribute the partial derivative:
Using the definition of discrete cross-correlation
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
:
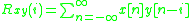
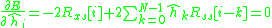
Rearrange the terms:
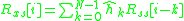
for all
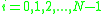
This system of N equations with N unknowns can be determined.
Derivation of the LMS algorithm
By relaxing the infinite sum of the Wiener filter to just the error at time, the LMS algorithm can be derived.The squared error can be expressed as:
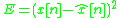
Using the Minimum mean-square error
Minimum mean-square error
In statistics and signal processing, a minimum mean square error estimator describes the approach which minimizes the mean square error , which is a common measure of estimator quality....
criterion, take the gradient:
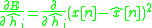
Apply chain rule and substitute definition of
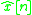
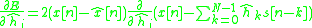
From this equation, we can derive an update equation for each
at every new using gradient descentGradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
and a step size
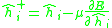
:which becomes, for i = 0, 1, ..., N-1,
This is the LMS update equation.