Sexual dimorphism measures
Encyclopedia
Although the subject of sexual dimorphism
is not in itself controversial, the measures by which it is assessed differ widely. Most of the measures are used on the assumption that a random variable
is considered so that probability distribution
s should be taken into account. In this review, a series of sexual dimorphism measures are discussed concerning both their definition and the probability law on which they are based. Most of them are sample functions, or statistics
, which account for only partial characteristics, for example the mean
or expected value
, of the distribution involved. Further, the most widely used measure fails to incorporate an inferential support.
is an important component of the morphological variation
in biological populations (see, e.g., Klein and Cruz-Uribe, 1983; Oxnard, 1987; Kelley, 1993). In higher Primates, sexual dimorphism is also related to some aspects of the social organization and behavior (Alexander et al., 1979; Clutton-Brock, 1985). Thus, it has been observed that the most dimorphic species tend to polygyny
and a social organization based on male dominance, whereas in the less dimorphic species, monogamy
and family groups are more common. Fleagle et al. (1980) and Kay (1982), on the other hand, have suggested that the behavior of extinct species can be inferred on the basis of sexual dimorphism and, e.g. Plavcan and van Shaick (1992) think that sex differences in size among primate species reflect processes of an ecological and social nature. Some references on sexual dimorphism regarding human populations can be seen in Lovejoy (1981), Borgognini Tarli and Repetto (1986) and Kappelman (1996)!
These biological facts do not appear to be controversial. However, they are based on a series of different sexual dimorphism measures, or indices. Sexual dimorphism, in most works, is measured on the assumption that a random variable
is being taken into account. This means that there is a law which accounts for the behavior of the whole set of values that compose the domain of the random variable, a law which is called distribution function
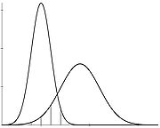
. Because both studies of sexual dimorphism aim at establishing differences, in some random variable, between sexes and the behavior of the random variable is accounted for by its distribution function, it seems reasonably clear that a sexual dimorphism study should be equivalent to a study whose main purpose is to determine to what extent the two distribution functions - one per sex - overlap (see shaded area in Fig. 1, where two normal distributions are represented).
can be seen. Perhaps, the most widely used is the quotient,
where
is the sample mean of one sex (e.g., male) and 
the corresponding mean of the other. Nonetheless, for instance,
have also been proposed.
Going over the works where these indices are used, one misses any reference to their parametric
counterpart. In other words, if we suppose that the quotient of two sample means is considered, no work can be found where, in order to make inferences, the way in which the quotient is used as a point estimate
of
is discussed.
By assuming that differences between populations are the objective to analyze, when quotients of sample means are used it is important to point out that the only feature of these populations that seems to be interesting is the mean parameter. However, a population has also variance, as well as a shape which is defined by its distribution function (notice that, in general, this function depends on parameters such as means or variances).
where
are sample variances and sample sizes, respectively.
Anyway, it is important to point out the following,
However, in sexual dimorphism analyses, it does not appear reasonably to assume that two independent random samples have been selected. Rather on the contrary, when we sample we select some random observations - making up one sample - that sometimes correspond to one sex and sometimes to the other.
functions (see Fig. 1). Therefore, it is a function of four parameters
(expected values and variances, respectively), and takes the shape of the two normals into account. Inman and Bradley (1989) have discussed this overlapping area as a measure to assess the distance between two normal densities.
Regarding inferences, Chakraborty and Majumder proposed a sample function constructed by considering the Laplace-DeMoivre's theorem (an application to binomial laws of the central limit theorem
). According to these authors, the variance of such a statistic is,
where
is the statistic, and 
(male, female) stand for the estimate of the probability of observing the measurement of an individual of the 
sex in some interval of the real line, and the sample size of the i sex, respectively. Notice that this implies that two independent random variables with binomial distributions have to be regarded. One of such variables is number of individuals of the f sex in a sample of size 
composed of individuals of the f sex, which seems nonsensical.
. Thus, if
is a random variable which is normally distributed among the females of a population and likewise this variable is normally distributed among the males of the population, then,
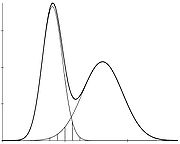
is the density of the mixture with two normal components, where
are the normal densities and the mixing proportions of both sexes, respectively. See an example in Fig. 2 where the thicker curve represents the mixture whereas the thinner curves are the 
functions.
It is from a population modelled like this that a random sample with individuals of both sexes can be selected. Note that on this sample tests which are based on the normal assumption cannot be applied since, in a mixture of two normal components, 
is not a normal density.
Josephson et al. limited themselves to considering two normal mixtures with the same component variances and mixing proportions. As a consequence, their proposal to measure sexual dimorphism is the difference between the mean parameters of the two normals involved. In estimating these central parameters, the procedure used by Josephson et al. is the one of Pearson's moments. Nowadays, the EM expectation maximization algorithm
(see McLachlan and Basford, 1988) and the MCMC Markov chain Monte Carlo
Bayesian procedure
(see Gilks et al., 1996) are the two competitors for estimating mixture parameters.
Possibly the main difference between considering two independent normal populations and a mixture model of two normal components is in the mixing proportions, which is the same as saying that in the two independent normal population model the interaction between sexes is ignored. This, in turn implies that probabilistic properties change (see Ipiña and Durand, 2000).
. This proposal computes the overlapping area between the 
and 
functions, which represent the contribution of each sex to the two normal components mixture (see shaded area in Fig. 2). Thus, 
can be written,
being the real line.
The smaller the overlapping area the greater the gap between the two functions
and 
, in which case the sexual dimorphism is greater. Obviously, this index is a function of the five parameters that characterize a mixture of two normal components (
. Its range is in the interval 
, and the interested reader can see, in the work of the authors who proposed the index, the way in which an interval estimate is constructed.
distance as a measure of sexual dimorphism. The authors use the following form of the statistic,
with
being sample cumulative distributions corresponding to two independent random samples.
Such a distance has the advantage of being applicable whatever the form of the random variable distributions concerned, yet they should be continuous. The use of this distance assumes that two populations are involved. Further, the Kolmogorov-Smirnov distance is a sample function whose aim is to test that the two samples under analysis have been selected from a single distribution. If one accepts the null hypothesis
, then there is not sexual dimorphism; otherwise, there is.
Sexual dimorphism
Sexual dimorphism is a phenotypic difference between males and females of the same species. Examples of such differences include differences in morphology, ornamentation, and behavior.-Examples:-Ornamentation / coloration:...
is not in itself controversial, the measures by which it is assessed differ widely. Most of the measures are used on the assumption that a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is considered so that probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s should be taken into account. In this review, a series of sexual dimorphism measures are discussed concerning both their definition and the probability law on which they are based. Most of them are sample functions, or statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, which account for only partial characteristics, for example the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
or expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, of the distribution involved. Further, the most widely used measure fails to incorporate an inferential support.
Introduction
It is widely known that sexual dimorphismSexual dimorphism
Sexual dimorphism is a phenotypic difference between males and females of the same species. Examples of such differences include differences in morphology, ornamentation, and behavior.-Examples:-Ornamentation / coloration:...
is an important component of the morphological variation
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
in biological populations (see, e.g., Klein and Cruz-Uribe, 1983; Oxnard, 1987; Kelley, 1993). In higher Primates, sexual dimorphism is also related to some aspects of the social organization and behavior (Alexander et al., 1979; Clutton-Brock, 1985). Thus, it has been observed that the most dimorphic species tend to polygyny
Polygyny
Polygyny is a form of marriage in which a man has two or more wives at the same time. In countries where the practice is illegal, the man is referred to as a bigamist or a polygamist...
and a social organization based on male dominance, whereas in the less dimorphic species, monogamy
Monogamy
Monogamy /Gr. μονός+γάμος - one+marriage/ a form of marriage in which an individual has only one spouse at any one time. In current usage monogamy often refers to having one sexual partner irrespective of marriage or reproduction...
and family groups are more common. Fleagle et al. (1980) and Kay (1982), on the other hand, have suggested that the behavior of extinct species can be inferred on the basis of sexual dimorphism and, e.g. Plavcan and van Shaick (1992) think that sex differences in size among primate species reflect processes of an ecological and social nature. Some references on sexual dimorphism regarding human populations can be seen in Lovejoy (1981), Borgognini Tarli and Repetto (1986) and Kappelman (1996)!
These biological facts do not appear to be controversial. However, they are based on a series of different sexual dimorphism measures, or indices. Sexual dimorphism, in most works, is measured on the assumption that a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is being taken into account. This means that there is a law which accounts for the behavior of the whole set of values that compose the domain of the random variable, a law which is called distribution function
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. Because both studies of sexual dimorphism aim at establishing differences, in some random variable, between sexes and the behavior of the random variable is accounted for by its distribution function, it seems reasonably clear that a sexual dimorphism study should be equivalent to a study whose main purpose is to determine to what extent the two distribution functions - one per sex - overlap (see shaded area in Fig. 1, where two normal distributions are represented).
Measures based on sample means
In Borgognini Tarli and Repetto (1986) an account of indices based on sample meansArithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
can be seen. Perhaps, the most widely used is the quotient,
where
is the sample mean of one sex (e.g., male) and the corresponding mean of the other. Nonetheless, for instance, have also been proposed.
Going over the works where these indices are used, one misses any reference to their parametric
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
counterpart. In other words, if we suppose that the quotient of two sample means is considered, no work can be found where, in order to make inferences, the way in which the quotient is used as a point estimate
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of
is discussed.
By assuming that differences between populations are the objective to analyze, when quotients of sample means are used it is important to point out that the only feature of these populations that seems to be interesting is the mean parameter. However, a population has also variance, as well as a shape which is defined by its distribution function (notice that, in general, this function depends on parameters such as means or variances).
Measures based on something more than sample means
Marini et al. (1999) have illustrated that it is a good idea to consider something other than sample means when sexual dimorphism is analyzed. Possibly, the main reason is that the intrasexual variability influences both the manifestation of dimorphism and its interpretation.Sample functions
It is likely that, within this type of indices, the one used the most is the well-known statistic with Student's t distribution (see, for instance, Green, 1989). Marini et al. (1999) have observed that variability among females seems to be lower than among males, so that it appears advisable to use the form of the Student's t statistic with degrees of freedom given by the Welch-Satterthwaite approximation,where
are sample variances and sample sizes, respectively.Anyway, it is important to point out the following,
- when this statistic is taken into account in sexual dimorphism studies, two normal populations are involved. From these populations two random samples are extracted, each one corresponding to a sex, and such samples are independent.
- when inferences are considered, what we are testing by using this statistic is that the difference between two mathematical expectations is a hypothesized value, say
However, in sexual dimorphism analyses, it does not appear reasonably to assume that two independent random samples have been selected. Rather on the contrary, when we sample we select some random observations - making up one sample - that sometimes correspond to one sex and sometimes to the other.
Taking parameters into account
Chakraborty and Majumder (1982) have proposed an index of sexual dimorphism that is the overlapping area - to be precise, its complement - of two normal densityProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
functions (see Fig. 1). Therefore, it is a function of four parameters
(expected values and variances, respectively), and takes the shape of the two normals into account. Inman and Bradley (1989) have discussed this overlapping area as a measure to assess the distance between two normal densities.Regarding inferences, Chakraborty and Majumder proposed a sample function constructed by considering the Laplace-DeMoivre's theorem (an application to binomial laws of the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
). According to these authors, the variance of such a statistic is,
where
is the statistic, and (male, female) stand for the estimate of the probability of observing the measurement of an individual of the sex in some interval of the real line, and the sample size of the i sex, respectively. Notice that this implies that two independent random variables with binomial distributions have to be regarded. One of such variables is number of individuals of the f sex in a sample of size composed of individuals of the f sex, which seems nonsensical.Mixture models
Authors such as Josephson et al. (1996) believe that the two sexes to be analyzed form a single population with a probabilistic behavior denominated a mixture of two normal populationsMixture model
In statistics, a mixture model is a probabilistic model for representing the presence of sub-populations within an overall population, without requiring that an observed data-set should identify the sub-population to which an individual observation belongs...
. Thus, if
is a random variable which is normally distributed among the females of a population and likewise this variable is normally distributed among the males of the population, then,is the density of the mixture with two normal components, where
are the normal densities and the mixing proportions of both sexes, respectively. See an example in Fig. 2 where the thicker curve represents the mixture whereas the thinner curves are the functions. is not a normal density.Josephson et al. limited themselves to considering two normal mixtures with the same component variances and mixing proportions. As a consequence, their proposal to measure sexual dimorphism is the difference between the mean parameters of the two normals involved. In estimating these central parameters, the procedure used by Josephson et al. is the one of Pearson's moments. Nowadays, the EM expectation maximization algorithm
Expectation-maximization algorithm
In statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
(see McLachlan and Basford, 1988) and the MCMC Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
Bayesian procedure
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
(see Gilks et al., 1996) are the two competitors for estimating mixture parameters.
Possibly the main difference between considering two independent normal populations and a mixture model of two normal components is in the mixing proportions, which is the same as saying that in the two independent normal population model the interaction between sexes is ignored. This, in turn implies that probabilistic properties change (see Ipiña and Durand, 2000).
The MI measure
Ipiña and Durand (2000, 2004) have proposed a measure of sexual dimorphism called. This proposal computes the overlapping area between the and functions, which represent the contribution of each sex to the two normal components mixture (see shaded area in Fig. 2). Thus, can be written, being the real line.The smaller the overlapping area the greater the gap between the two functions
and , in which case the sexual dimorphism is greater. Obviously, this index is a function of the five parameters that characterize a mixture of two normal components (. Its range is in the interval , and the interested reader can see, in the work of the authors who proposed the index, the way in which an interval estimate is constructed.Measures based on non-parametric methods
Marini et al. (1999) have suggested the Kolmogorov-SmirnovKolmogorov-Smirnov test
In statistics, the Kolmogorov–Smirnov test is a nonparametric test for the equality of continuous, one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution , or to compare two samples...
distance as a measure of sexual dimorphism. The authors use the following form of the statistic,
with
being sample cumulative distributions corresponding to two independent random samples.Such a distance has the advantage of being applicable whatever the form of the random variable distributions concerned, yet they should be continuous. The use of this distance assumes that two populations are involved. Further, the Kolmogorov-Smirnov distance is a sample function whose aim is to test that the two samples under analysis have been selected from a single distribution. If one accepts the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
, then there is not sexual dimorphism; otherwise, there is.
See also
- Bateman's principleBateman's principleIn biology, Bateman's principle is the theory that females almost always invest more energy into producing offspring than males invest, and therefore in most species females are a limiting resource over which the other sex will compete...
- Digit ratioDigit ratioThe digit ratio is the ratio of the lengths of different digits or fingers typically measured from the bottom crease where the finger joins the hand to the tip of the finger. It has been suggested by some scientists that the ratio of two digits in particular, the 2nd and 4th , is affected by...
- Gender differencesGender differencesA sex difference is a distinction of biological and/or physiological characteristics associated with either males or females of a species. These can be of several types, including direct and indirect. Direct being the direct result of differences prescribed by the Y-chromosome, and indirect being...
- Sexual dimorphismSexual dimorphismSexual dimorphism is a phenotypic difference between males and females of the same species. Examples of such differences include differences in morphology, ornamentation, and behavior.-Examples:-Ornamentation / coloration:...