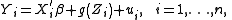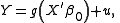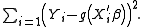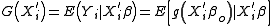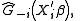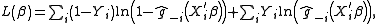Semiparametric regression
Encyclopedia
In statistics
, semiparametric regression includes regression
models that combine parametric
and nonparametric
models. They are often used in situations where the fully nonparametric model may not perform well or when the researcher wants to use a parametric model but the functional form with respect to a subset of the regressors or the density of the errors is not known. Semiparametric regression models are a particular type of semiparametric modelling and, since semiparametric models contain a parametric component, they rely on parametric assumptions and may be misspecified
and inconsistent
, just like a fully parametric model.
where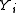 is the dependent variable,
is the dependent variable, 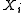 and
and 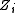 are
are 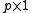 vectors of explanatory variables,
vectors of explanatory variables, 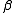 is a
is a 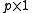 vector of unknown parameters and
vector of unknown parameters and 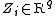 . The parametric part of the partially linear model is given by the parameter vector
. The parametric part of the partially linear model is given by the parameter vector 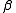 while the nonparametric part is the unknown function
while the nonparametric part is the unknown function  . The data is assumed to be i.i.d. with
. The data is assumed to be i.i.d. with 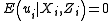 and the model allows for a conditionally heteroskedastic error process
and the model allows for a conditionally heteroskedastic error process 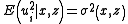 of unknown form. This type of model was proposed by Robinson (1988) and extended to handle categorical covariates by Racine and Liu (2007).
of unknown form. This type of model was proposed by Robinson (1988) and extended to handle categorical covariates by Racine and Liu (2007).
This method is implemented by obtaining a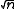 consistent estimator of
consistent estimator of 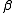 and then deriving an estimator of
and then deriving an estimator of 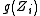 from the nonparametric regression
from the nonparametric regression
of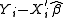 on
on  using an appropriate nonparametric regression method.
using an appropriate nonparametric regression method.
takes the form
where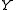 ,
, 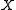 and
and 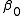 are defined as earlier and the error term
are defined as earlier and the error term  satisfies
satisfies 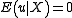 . The single index model takes its name from the parametric part of the model
. The single index model takes its name from the parametric part of the model 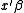 which is a scalar single index. The nonparametric part is the unknown function
which is a scalar single index. The nonparametric part is the unknown function 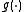 .
.
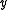 is continuous. Given a known form for the function
is continuous. Given a known form for the function 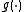 ,
,  could be estimated using the nonlinear least squares
could be estimated using the nonlinear least squares
method to minimize the function
Since the functional form of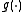 is not known, we need to estimate it. For a given value for
is not known, we need to estimate it. For a given value for 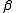 an estimate of the function
an estimate of the function
using kernel
method. Ichimura (1993) proposes estimating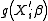 with
with
the leave-one-out
nonparametric kernel
estimator of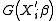 .
.
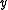 is binary and
is binary and 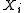 and
and 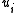 are assumed to be independent, Klein and Spady (1993) propose a technique for estimating
are assumed to be independent, Klein and Spady (1993) propose a technique for estimating 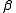 using maximum likelihood
using maximum likelihood
methods. The log-likelihood function is given by
where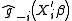 is the leave-one-out
is the leave-one-out
estimator.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, semiparametric regression includes regression
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
models that combine parametric
Parametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...
and nonparametric
Kernel regression
The kernel regression is a non-parametric technique in statistics to estimate the conditional expectation of a random variable. The objective is to find a non-linear relation between a pair of random variables X and Y....
models. They are often used in situations where the fully nonparametric model may not perform well or when the researcher wants to use a parametric model but the functional form with respect to a subset of the regressors or the density of the errors is not known. Semiparametric regression models are a particular type of semiparametric modelling and, since semiparametric models contain a parametric component, they rely on parametric assumptions and may be misspecified
Specification (regression)
In regression analysis and related fields such as econometrics, specification is the process of converting a theory into a regression model. This process consists of selecting an appropriate functional form for the model and choosing which variables to include. Model specification is one of the...
and inconsistent
Consistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
, just like a fully parametric model.
Methods
Many different semiparametric regression methods have been proposed and developed. The most popular methods are the partially linear, index and varying coefficient models.Partially linear models
A partially linear model is given bywhere
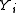 is the dependent variable,
is the dependent variable, 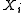 and
and 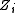 are
are 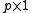 vectors of explanatory variables,
vectors of explanatory variables, 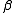 is a
is a 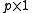 vector of unknown parameters and
vector of unknown parameters and 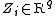 . The parametric part of the partially linear model is given by the parameter vector
. The parametric part of the partially linear model is given by the parameter vector 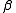 while the nonparametric part is the unknown function
while the nonparametric part is the unknown function  . The data is assumed to be i.i.d. with
. The data is assumed to be i.i.d. with 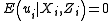 and the model allows for a conditionally heteroskedastic error process
and the model allows for a conditionally heteroskedastic error process 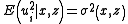 of unknown form. This type of model was proposed by Robinson (1988) and extended to handle categorical covariates by Racine and Liu (2007).
of unknown form. This type of model was proposed by Robinson (1988) and extended to handle categorical covariates by Racine and Liu (2007).This method is implemented by obtaining a
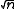 consistent estimator of
consistent estimator of 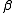 and then deriving an estimator of
and then deriving an estimator of 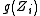 from the nonparametric regression
from the nonparametric regressionKernel regression
The kernel regression is a non-parametric technique in statistics to estimate the conditional expectation of a random variable. The objective is to find a non-linear relation between a pair of random variables X and Y....
of
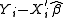 on
on  using an appropriate nonparametric regression method.
using an appropriate nonparametric regression method.Index models
A single index modelSingle Index Model
The single-index model is a simple asset pricing model commonly used in the finance industry to measure risk and return of a stock. Mathematically the SIM is expressed as:...
takes the form
where
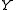 ,
, 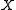 and
and 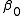 are defined as earlier and the error term
are defined as earlier and the error term  satisfies
satisfies 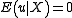 . The single index model takes its name from the parametric part of the model
. The single index model takes its name from the parametric part of the model 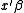 which is a scalar single index. The nonparametric part is the unknown function
which is a scalar single index. The nonparametric part is the unknown function 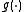 .
.Ichimura's method
The single index model method developed by Ichimura (1993) is as follows. Consider the situation in which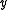 is continuous. Given a known form for the function
is continuous. Given a known form for the function 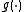 ,
,  could be estimated using the nonlinear least squares
could be estimated using the nonlinear least squaresNon-linear least squares
Non-linear least squares is the form of least squares analysis which is used to fit a set of m observations with a model that is non-linear in n unknown parameters . It is used in some forms of non-linear regression. The basis of the method is to approximate the model by a linear one and to...
method to minimize the function
Since the functional form of
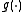 is not known, we need to estimate it. For a given value for
is not known, we need to estimate it. For a given value for 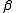 an estimate of the function
an estimate of the functionusing kernel
Kernel density estimation
In statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
method. Ichimura (1993) proposes estimating
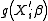 with
withthe leave-one-out
Resampling (statistics)
In statistics, resampling is any of a variety of methods for doing one of the following:# Estimating the precision of sample statistics by using subsets of available data or drawing randomly with replacement from a set of data points # Exchanging labels on data points when performing significance...
nonparametric kernel
Kernel density estimation
In statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
estimator of
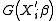 .
.Klein and Spady's estimator
If the dependant variable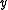 is binary and
is binary and 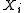 and
and 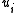 are assumed to be independent, Klein and Spady (1993) propose a technique for estimating
are assumed to be independent, Klein and Spady (1993) propose a technique for estimating 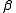 using maximum likelihood
using maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
methods. The log-likelihood function is given by
where
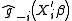 is the leave-one-out
is the leave-one-outResampling (statistics)
In statistics, resampling is any of a variety of methods for doing one of the following:# Estimating the precision of sample statistics by using subsets of available data or drawing randomly with replacement from a set of data points # Exchanging labels on data points when performing significance...
estimator.
Smooth coefficient\varying coefficient models
Hastie and Tibshirani (1993) propose a smooth coefficient model given by-

where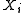 is a
is a 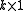 vector and
vector and 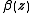 is a vector of unspecified smooth functions of
is a vector of unspecified smooth functions of  .
.
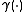 may be expressed as
may be expressed as
-