
Self-consistent mean field (biology)
Encyclopedia
The self-consistent mean field (SCMF) method is an adaptation of mean field theory
used in protein structure prediction
to determine the optimal amino acid
side chain
packing given a fixed protein backbone
. It is faster but less accurate than dead-end elimination
and is generally used in situations where the protein of interest is too large for the problem to be tractable by DEE.
s of each side chain into a set of rotamers for each position in the protein sequence. The method iteratively develops a probabilistic description of the relative population of each possible rotamer at each position, and the probability of a given structure is defined as a function of the probabilities of its individual rotamer components.
The basic requirements for an effective SCMF implementation are:
The process is generally initialized with a uniform probability distribution over the rotamers - that is, if there are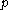 rotamers at the
rotamers at the 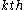 position in the protein, then the probability of any individual rotamer
position in the protein, then the probability of any individual rotamer 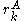 is
is 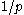 . The conversion between energies and probabilities is generally accomplished via the Boltzmann distribution
. The conversion between energies and probabilities is generally accomplished via the Boltzmann distribution
, which introduces a temperature factor (thus making the method amenable to simulated annealing
). Lower temperatures increase the likelihood of converging to a single solution, rather than to a small subpopulation of solutions.
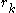 is dependent on the "mean-field" energy of the other positions - that is, at every other position, each rotamer's energy contribution is proportional to its probability. For a protein of length
is dependent on the "mean-field" energy of the other positions - that is, at every other position, each rotamer's energy contribution is proportional to its probability. For a protein of length 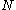 with
with 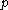 rotamers per residue, the energy at the current iteration is described by the following expression. Note that for clarity, the mean-field energy at iteration
rotamers per residue, the energy at the current iteration is described by the following expression. Note that for clarity, the mean-field energy at iteration 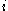 is denoted by
is denoted by 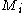 , whereas the precomputed energies are denoted by
, whereas the precomputed energies are denoted by 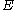 , and the probability of a given rotamer is denoted by
, and the probability of a given rotamer is denoted by 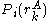 .
.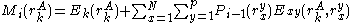
These mean-field energies are used to update the probabilities through the Boltzmann law:
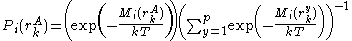
where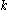 is the Boltzmann constant and
is the Boltzmann constant and 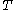 is the temperature factor.
is the temperature factor.
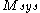 consists of two sums:
consists of two sums:
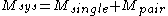
where the addends are defined as: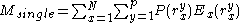
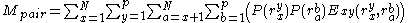
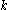 in the protein, and a probability of zero for all other rotamers at each position. Convergence to a unique solution requires probabilities close to 1 for exactly one rotamer at each position. In practice, especially when higher temperatures are used, the algorithm instead identifies a small number of high-probability rotamers at each position, allowing the resulting conformations' relative energies to then be enumerated (based on the precomputed energies, not on those derived from the mean-field approximation). One way to improve convergence is to run again at a lower temperature using the probabilities calculated from a previous higher-temperature run.
in the protein, and a probability of zero for all other rotamers at each position. Convergence to a unique solution requires probabilities close to 1 for exactly one rotamer at each position. In practice, especially when higher temperatures are used, the algorithm instead identifies a small number of high-probability rotamers at each position, allowing the resulting conformations' relative energies to then be enumerated (based on the precomputed energies, not on those derived from the mean-field approximation). One way to improve convergence is to run again at a lower temperature using the probabilities calculated from a previous higher-temperature run.
Mean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
used in protein structure prediction
Protein structure prediction
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse...
to determine the optimal amino acid
Amino acid
Amino acids are molecules containing an amine group, a carboxylic acid group and a side-chain that varies between different amino acids. The key elements of an amino acid are carbon, hydrogen, oxygen, and nitrogen...
side chain
Side chain
In organic chemistry and biochemistry, a side chain is a chemical group that is attached to a core part of the molecule called "main chain" or backbone. The placeholder R is often used as a generic placeholder for alkyl group side chains in chemical structure diagrams. To indicate other non-carbon...
packing given a fixed protein backbone
Tertiary structure
In biochemistry and molecular biology, the tertiary structure of a protein or any other macromolecule is its three-dimensional structure, as defined by the atomic coordinates.-Relationship to primary structure:...
. It is faster but less accurate than dead-end elimination
Dead-end elimination
The dead-end elimination algorithm ' is a method for minimizing a function over a discrete set of independent variables. The basic idea is to identify "dead ends", i.e., "bad" combinations of variables that cannot possibly yield the global minimum and to refrain from searching such combinations...
and is generally used in situations where the protein of interest is too large for the problem to be tractable by DEE.
General principles
Like dead-end elimination, the SCMF method explores conformational space by discretizing the dihedral angleDihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
s of each side chain into a set of rotamers for each position in the protein sequence. The method iteratively develops a probabilistic description of the relative population of each possible rotamer at each position, and the probability of a given structure is defined as a function of the probabilities of its individual rotamer components.
The basic requirements for an effective SCMF implementation are:
- A well-defined finite set of discrete independent variables
- A precomputed numerical value (considered the "energy") associated with each element in the set of variables, and associated with each binary element pair
- An initial probability distribution describing the starting population of each individual rotamer
- A way of updating rotamer energies and probabilities as a function of the mean-field energy
The process is generally initialized with a uniform probability distribution over the rotamers - that is, if there are
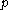 rotamers at the
rotamers at the 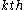 position in the protein, then the probability of any individual rotamer
position in the protein, then the probability of any individual rotamer 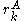 is
is 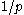 . The conversion between energies and probabilities is generally accomplished via the Boltzmann distribution
. The conversion between energies and probabilities is generally accomplished via the Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
, which introduces a temperature factor (thus making the method amenable to simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
). Lower temperatures increase the likelihood of converging to a single solution, rather than to a small subpopulation of solutions.
Mean-field energies
The energy of an individual rotamer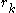 is dependent on the "mean-field" energy of the other positions - that is, at every other position, each rotamer's energy contribution is proportional to its probability. For a protein of length
is dependent on the "mean-field" energy of the other positions - that is, at every other position, each rotamer's energy contribution is proportional to its probability. For a protein of length 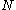 with
with 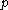 rotamers per residue, the energy at the current iteration is described by the following expression. Note that for clarity, the mean-field energy at iteration
rotamers per residue, the energy at the current iteration is described by the following expression. Note that for clarity, the mean-field energy at iteration 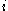 is denoted by
is denoted by 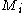 , whereas the precomputed energies are denoted by
, whereas the precomputed energies are denoted by 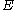 , and the probability of a given rotamer is denoted by
, and the probability of a given rotamer is denoted by 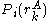 .
.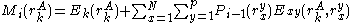
These mean-field energies are used to update the probabilities through the Boltzmann law:
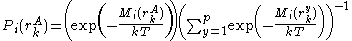
where
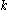 is the Boltzmann constant and
is the Boltzmann constant and 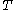 is the temperature factor.
is the temperature factor.Energy of the system
Although computing the system energy is not required in carrying out the SCMF method, it is useful to know the overall energies of the converged results. The system energy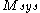 consists of two sums:
consists of two sums: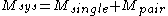
where the addends are defined as:
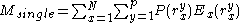
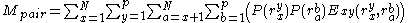
Convergence
Perfect convergence for the SCMF method would result in a probability of 1 for exactly one rotamer at each position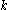 in the protein, and a probability of zero for all other rotamers at each position. Convergence to a unique solution requires probabilities close to 1 for exactly one rotamer at each position. In practice, especially when higher temperatures are used, the algorithm instead identifies a small number of high-probability rotamers at each position, allowing the resulting conformations' relative energies to then be enumerated (based on the precomputed energies, not on those derived from the mean-field approximation). One way to improve convergence is to run again at a lower temperature using the probabilities calculated from a previous higher-temperature run.
in the protein, and a probability of zero for all other rotamers at each position. Convergence to a unique solution requires probabilities close to 1 for exactly one rotamer at each position. In practice, especially when higher temperatures are used, the algorithm instead identifies a small number of high-probability rotamers at each position, allowing the resulting conformations' relative energies to then be enumerated (based on the precomputed energies, not on those derived from the mean-field approximation). One way to improve convergence is to run again at a lower temperature using the probabilities calculated from a previous higher-temperature run.
