
Dead-end elimination
Encyclopedia
The dead-end elimination algorithm (DEE) is a method for minimizing
a function over a discrete set of independent variables. The basic idea is to identify "dead ends", i.e., "bad" combinations of variables that cannot possibly yield the global minimum and to refrain from searching such combinations further. Hence, dead-end elimination is a mirror image of dynamic programming
, in which "good" combinations are identified and explored further. Although the method itself is general, it has been developed and applied mainly to the problems of predicting
and designing
the structures of protein
s. The original description and proof of the dead-end elimination theorem can be found in .
Note that the criteria can easily be reversed to identify the maximum of a given function as well.
by minimizing an energy function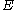 . The dihedral angle
. The dihedral angle
search space of the side chains is restricted to a discrete set of rotamers for each amino acid
position in the protein (which is, obviously, of fixed length). The original DEE description included criteria for the elimination of single rotamers and of rotamer pairs, although this can be expanded.
In the following discussion, let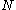 be the length of the protein and let
be the length of the protein and let 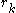 represent the rotamer of the
represent the rotamer of the 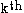 side chain. Since atoms in proteins are assumed to interact only by two-body potential
side chain. Since atoms in proteins are assumed to interact only by two-body potential
s, the energy may be written
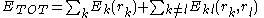
Where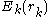 represents the "self-energy" of a particular rotamer
represents the "self-energy" of a particular rotamer 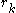 , and
, and 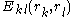 represents the "pair energy" of the rotamers
represents the "pair energy" of the rotamers 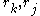 .
.
Also note that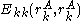 (that is, the pair energy between a rotamer and itself) is taken to be zero, and thus does not affect the summations. This notation simplifies the description of the pairs criterion below.
(that is, the pair energy between a rotamer and itself) is taken to be zero, and thus does not affect the summations. This notation simplifies the description of the pairs criterion below.
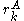 of sidechain
of sidechain 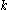 cannot possibly give a better energy than another rotamer
cannot possibly give a better energy than another rotamer 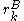 of the same sidechain, then rotamer A can be eliminated from further consideration, which reduces the search space. Mathematically, this condition is expressed by the inequality
of the same sidechain, then rotamer A can be eliminated from further consideration, which reduces the search space. Mathematically, this condition is expressed by the inequality

where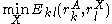 is the minimum (best) energy possible between rotamer
is the minimum (best) energy possible between rotamer 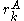 of sidechain
of sidechain 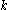 and any rotamer X of side chain
and any rotamer X of side chain 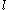 . Similarly,
. Similarly, 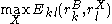 is the maximum (worst) energy possible between rotamer
is the maximum (worst) energy possible between rotamer  of sidechain
of sidechain 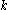 and any rotamer X of side chain
and any rotamer X of side chain 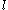 .
.
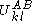 that is the intrinsic energy of a pair of rotamers
that is the intrinsic energy of a pair of rotamers 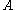 and
and 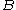 at positions
at positions 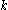 and
and 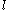 , respectively
, respectively
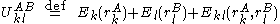
A given pair of rotamers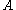 and
and 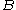 at positions
at positions 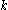 and
and 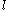 , respectively, cannot both be in the final solution (although one or the other may be) if there is another pair
, respectively, cannot both be in the final solution (although one or the other may be) if there is another pair 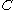 and
and 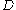 that always gives a better energy. Expressed mathematically,
that always gives a better energy. Expressed mathematically,
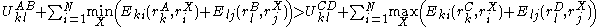
where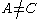 ,
, 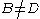 and
and 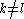 .
.
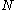 , the matrices of precomputed energies can become costly to store. Let
, the matrices of precomputed energies can become costly to store. Let 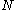 be the number of amino acid positions, as above, and let
be the number of amino acid positions, as above, and let 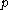 be the number of rotamers at each position (this is usually, but not necessarily, constant over all positions). Each self-energy matrix for a given position requires
be the number of rotamers at each position (this is usually, but not necessarily, constant over all positions). Each self-energy matrix for a given position requires 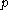 entries, so the total number of self-energies to store is
entries, so the total number of self-energies to store is 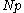 . Each pair energy matrix between two positions
. Each pair energy matrix between two positions 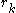 and
and 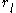 , for
, for 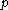 discrete rotamers at each position, requires a
discrete rotamers at each position, requires a 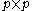 matrix. This makes the total number of entries in an unreduced pair matrix
matrix. This makes the total number of entries in an unreduced pair matrix 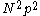 . This can be trimmed somewhat, at the cost of additional complexity in implementation, because pair energies are symmetrical and the pair energy between a rotamer and itself is zero.
. This can be trimmed somewhat, at the cost of additional complexity in implementation, because pair energies are symmetrical and the pair energy between a rotamer and itself is zero.
Given this model, it is clear that the DEE algorithm is guaranteed to find the optimal solution; that is, it is a global optimization
process. The single-rotamer search scales quadratically
in time with total number of rotamers. The pair search scales cubically and is the slowest part of the algorithm (aside from energy calculations). This is a dramatic improvement over the brute-force enumeration which scales as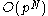 .
.
A large-scale benchmark
of DEE compared with alternative methods of protein structure prediction
and design finds that DEE reliably converges to the optimal solution for protein lengths for which it runs in a reasonable amount of time. It significantly outperforms the alternatives under consideration, which involved techniques derived from mean field theory
, genetic algorithm
s, and the Monte Carlo method
. However, the other algorithms are appreciably faster than DEE and thus can be applied to larger and more complex problems; their relative accuracy can be extrapolated from a comparison to the DEE solution within the scope of problems accessible to DEE.
Protein design
The preceding discussion implicitly assumed that the rotamers 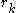 are all different orientations of the same amino acid side chain. That is, the sequence of the protein was assumed to be fixed. It is also possible to allow multiple side chains to "compete" over a position
are all different orientations of the same amino acid side chain. That is, the sequence of the protein was assumed to be fixed. It is also possible to allow multiple side chains to "compete" over a position 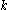 by including both types of side chains in the set of rotamers for that position. This allows a novel sequence to be designed onto a given protein backbone. A short zinc finger
by including both types of side chains in the set of rotamers for that position. This allows a novel sequence to be designed onto a given protein backbone. A short zinc finger
protein fold has been redesigned this way. However, this greatly increases the number of rotamers per position and still requires a fixed protein length.
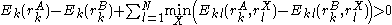
Thus rotamer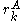 can be eliminated if any alternative rotamer from the set at
can be eliminated if any alternative rotamer from the set at 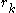 contributes less to the total energy than
contributes less to the total energy than 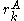 . This is an improvement over the original criterion, which requires comparison of the best possible (that is, the smallest) energy contribution from
. This is an improvement over the original criterion, which requires comparison of the best possible (that is, the smallest) energy contribution from 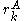 with the worst possible contribution from an alternative rotamer.
with the worst possible contribution from an alternative rotamer.
An extended discussion of elaborate DEE criteria and a benchmark of their relative performance can be found in .
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
a function over a discrete set of independent variables. The basic idea is to identify "dead ends", i.e., "bad" combinations of variables that cannot possibly yield the global minimum and to refrain from searching such combinations further. Hence, dead-end elimination is a mirror image of dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
, in which "good" combinations are identified and explored further. Although the method itself is general, it has been developed and applied mainly to the problems of predicting
Protein structure prediction
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse...
and designing
Protein design
Protein design is the design of new protein molecules, either from scratch or by making calculated variations on a known structure. The use of rational design techniques for proteins is a major aspect of protein engineering....
the structures of protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
s. The original description and proof of the dead-end elimination theorem can be found in .
Basic requirements
An effective DEE implementation requires four pieces of information:- A well-defined finite set of discrete independent variables
- A precomputed numerical value (considered the "energy") associated with each element in the set of variables (and possibly with their pairs, triples, etc.)
- A criterion or criteria for determining when an element is a "dead end", that is, when it cannot possibly be a member of the solution set
- An objective function (considered the "energy function") to be minimized
Note that the criteria can easily be reversed to identify the maximum of a given function as well.
Applications to protein structure prediction
Dead-end elimination has been used effectively to predict the structure of side chains on a given protein backbone structureTertiary structure
In biochemistry and molecular biology, the tertiary structure of a protein or any other macromolecule is its three-dimensional structure, as defined by the atomic coordinates.-Relationship to primary structure:...
by minimizing an energy function
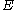 . The dihedral angle
. The dihedral angleDihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
search space of the side chains is restricted to a discrete set of rotamers for each amino acid
Amino acid
Amino acids are molecules containing an amine group, a carboxylic acid group and a side-chain that varies between different amino acids. The key elements of an amino acid are carbon, hydrogen, oxygen, and nitrogen...
position in the protein (which is, obviously, of fixed length). The original DEE description included criteria for the elimination of single rotamers and of rotamer pairs, although this can be expanded.
In the following discussion, let
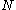 be the length of the protein and let
be the length of the protein and let 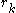 represent the rotamer of the
represent the rotamer of the 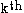 side chain. Since atoms in proteins are assumed to interact only by two-body potential
side chain. Since atoms in proteins are assumed to interact only by two-body potentialPotential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
s, the energy may be written
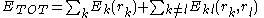
Where
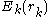 represents the "self-energy" of a particular rotamer
represents the "self-energy" of a particular rotamer 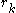 , and
, and 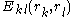 represents the "pair energy" of the rotamers
represents the "pair energy" of the rotamers 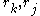 .
.Also note that
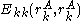 (that is, the pair energy between a rotamer and itself) is taken to be zero, and thus does not affect the summations. This notation simplifies the description of the pairs criterion below.
(that is, the pair energy between a rotamer and itself) is taken to be zero, and thus does not affect the summations. This notation simplifies the description of the pairs criterion below.Singles elimination criterion
If a particular rotamer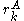 of sidechain
of sidechain 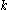 cannot possibly give a better energy than another rotamer
cannot possibly give a better energy than another rotamer 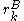 of the same sidechain, then rotamer A can be eliminated from further consideration, which reduces the search space. Mathematically, this condition is expressed by the inequality
of the same sidechain, then rotamer A can be eliminated from further consideration, which reduces the search space. Mathematically, this condition is expressed by the inequality
where
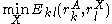 is the minimum (best) energy possible between rotamer
is the minimum (best) energy possible between rotamer 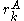 of sidechain
of sidechain 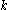 and any rotamer X of side chain
and any rotamer X of side chain 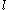 . Similarly,
. Similarly, 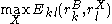 is the maximum (worst) energy possible between rotamer
is the maximum (worst) energy possible between rotamer  of sidechain
of sidechain 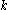 and any rotamer X of side chain
and any rotamer X of side chain 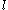 .
.Pairs elimination criterion
The pairs criterion is more difficult to describe and to implement, but it adds significant eliminating power. For brevity, we define the shorthand variable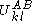 that is the intrinsic energy of a pair of rotamers
that is the intrinsic energy of a pair of rotamers 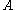 and
and 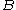 at positions
at positions 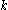 and
and 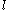 , respectively
, respectively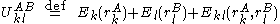
A given pair of rotamers
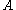 and
and 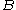 at positions
at positions 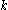 and
and 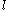 , respectively, cannot both be in the final solution (although one or the other may be) if there is another pair
, respectively, cannot both be in the final solution (although one or the other may be) if there is another pair 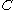 and
and 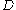 that always gives a better energy. Expressed mathematically,
that always gives a better energy. Expressed mathematically,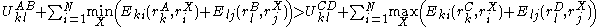
where
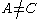 ,
, 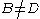 and
and 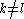 .
.Energy matrices
For large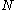 , the matrices of precomputed energies can become costly to store. Let
, the matrices of precomputed energies can become costly to store. Let 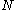 be the number of amino acid positions, as above, and let
be the number of amino acid positions, as above, and let 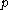 be the number of rotamers at each position (this is usually, but not necessarily, constant over all positions). Each self-energy matrix for a given position requires
be the number of rotamers at each position (this is usually, but not necessarily, constant over all positions). Each self-energy matrix for a given position requires 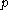 entries, so the total number of self-energies to store is
entries, so the total number of self-energies to store is 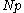 . Each pair energy matrix between two positions
. Each pair energy matrix between two positions 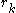 and
and 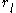 , for
, for 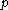 discrete rotamers at each position, requires a
discrete rotamers at each position, requires a 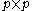 matrix. This makes the total number of entries in an unreduced pair matrix
matrix. This makes the total number of entries in an unreduced pair matrix 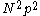 . This can be trimmed somewhat, at the cost of additional complexity in implementation, because pair energies are symmetrical and the pair energy between a rotamer and itself is zero.
. This can be trimmed somewhat, at the cost of additional complexity in implementation, because pair energies are symmetrical and the pair energy between a rotamer and itself is zero.Implementation and efficiency
The above two criteria are normally applied iteratively until convergence, defined as the point at which no more rotamers or pairs can be eliminated. Since this is normally a reduction in the sample space by many orders of magnitude, simple enumeration will suffice to determine the minimum within this pared-down set.Given this model, it is clear that the DEE algorithm is guaranteed to find the optimal solution; that is, it is a global optimization
Global optimization
Global optimization is a branch of applied mathematics and numerical analysis that deals with the optimization of a function or a set of functions to some criteria.- General :The most common form is the minimization of one real-valued function...
process. The single-rotamer search scales quadratically
Quadratic growth
In mathematics, a function or sequence is said to exhibit quadratic growth when its values are proportional to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity...
in time with total number of rotamers. The pair search scales cubically and is the slowest part of the algorithm (aside from energy calculations). This is a dramatic improvement over the brute-force enumeration which scales as
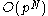 .
.A large-scale benchmark
Benchmark (computing)
In computing, a benchmark is the act of running a computer program, a set of programs, or other operations, in order to assess the relative performance of an object, normally by running a number of standard tests and trials against it...
of DEE compared with alternative methods of protein structure prediction
Protein structure prediction
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse...
and design finds that DEE reliably converges to the optimal solution for protein lengths for which it runs in a reasonable amount of time. It significantly outperforms the alternatives under consideration, which involved techniques derived from mean field theory
Mean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
, genetic algorithm
Genetic algorithm
A genetic algorithm is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems...
s, and the Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
. However, the other algorithms are appreciably faster than DEE and thus can be applied to larger and more complex problems; their relative accuracy can be extrapolated from a comparison to the DEE solution within the scope of problems accessible to DEE.
Protein designProtein designProtein design is the design of new protein molecules, either from scratch or by making calculated variations on a known structure. The use of rational design techniques for proteins is a major aspect of protein engineering....
The preceding discussion implicitly assumed that the rotamers 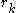 are all different orientations of the same amino acid side chain. That is, the sequence of the protein was assumed to be fixed. It is also possible to allow multiple side chains to "compete" over a position
are all different orientations of the same amino acid side chain. That is, the sequence of the protein was assumed to be fixed. It is also possible to allow multiple side chains to "compete" over a position 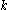 by including both types of side chains in the set of rotamers for that position. This allows a novel sequence to be designed onto a given protein backbone. A short zinc finger
by including both types of side chains in the set of rotamers for that position. This allows a novel sequence to be designed onto a given protein backbone. A short zinc fingerZinc finger
Zinc fingers are small protein structural motifs that can coordinate one or more zinc ions to help stabilize their folds. They can be classified into several different structural families and typically function as interaction modules that bind DNA, RNA, proteins, or small molecules...
protein fold has been redesigned this way. However, this greatly increases the number of rotamers per position and still requires a fixed protein length.
Generalizations
More powerful and more general criteria have been introduced that improve both the efficiency and the eliminating power of the method for both prediction and design applications. One example is a refinement of the singles elimination criterion known as the Goldstein criterion, which arises from fairly straightforward algebraic manipulation before applying the minimization: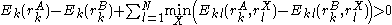
Thus rotamer
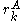 can be eliminated if any alternative rotamer from the set at
can be eliminated if any alternative rotamer from the set at 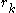 contributes less to the total energy than
contributes less to the total energy than 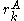 . This is an improvement over the original criterion, which requires comparison of the best possible (that is, the smallest) energy contribution from
. This is an improvement over the original criterion, which requires comparison of the best possible (that is, the smallest) energy contribution from 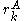 with the worst possible contribution from an alternative rotamer.
with the worst possible contribution from an alternative rotamer.An extended discussion of elaborate DEE criteria and a benchmark of their relative performance can be found in .

