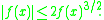Self-concordant function
Encyclopedia
In optimization
, a self-concordant function is a function
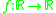for which
A function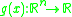
is self-concordant if its restriction to any arbitrary line is self-concordant.
s, and scalar multiplication by a value greater than one.
. Self-concordant barrier functions are used to develop the barrier function
s used in interior point method
s for convex and nonlinear optimization.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, a self-concordant function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
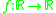for which
A function
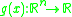is self-concordant if its restriction to any arbitrary line is self-concordant.Properties
Self concordance is preserved under addition, affine transformationAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s, and scalar multiplication by a value greater than one.
Applications
Among other things, self-concordant functions are useful in the analysis of Newton's methodNewton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. Self-concordant barrier functions are used to develop the barrier function
Barrier function
In constrained optimization, a field of mathematics, a barrier function is a continuous function whose value on a point increases to infinity as the point approaches the boundary of the feasible region . It is used as a penalizing term for violations of constraints...
s used in interior point method
Interior point method
Interior point methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems.The interior point method was invented by John von Neumann...
s for convex and nonlinear optimization.