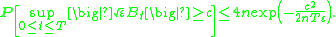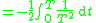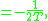Schilder's theorem
Encyclopedia
In mathematics
, Schilder's theorem is a result in the large deviations theory
of stochastic process
es. Roughly speaking, Schilder's theorem gives an estimate for the probability that a (scaled-down) sample path of Brownian motion
will stray far from the mean path (which is constant with value 0). This statement is made precise using rate function
s. Schilder's theorem is generalized by the Freidlin–Wentzell theorem for Itō diffusion
s.
al Euclidean space
Rd starting at the origin, 0 ∈ Rd; let W denote the law
of B, i.e. classical Wiener measure. For ε > 0, let Wε denote the law of the rescaled process (√ε)B. Then, on the Banach space
C0 = C0([0, T]; Rd) of continuous functions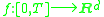
such that 
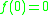, equipped with the supremum norm ||·||∞, the probability measure
s Wε satisfy the large deviations principle with good rate function I : C0 → R ∪ {+∞} given by
if ω is absolutely continuous, and I(ω) = +∞ otherwise. In other words, for every open set
G ⊆ C0 and every closed set
F ⊆ C0,
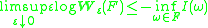
and
as c tends to infinity. Here Bc(0; ||·||∞) denotes the open ball of radius c about the zero function in C0, taken with respect to the supremum norm. First note that
Since the rate function is continuous on A, Schilder's theorem yields
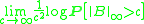
making use of the fact that the infimum
over paths in the collection A is attained for ω(t) = t ⁄ T. This result can be heuristically interpreted as saying that, for large c and/or large T
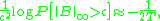
or, in other words,
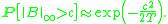
In fact, the above probability can be estimated more precisely as follows: for B a standard Brownian motion in Rn, and any T, c and ε > 0, it holds that
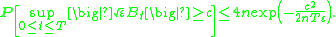
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Schilder's theorem is a result in the large deviations theory
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es. Roughly speaking, Schilder's theorem gives an estimate for the probability that a (scaled-down) sample path of Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
will stray far from the mean path (which is constant with value 0). This statement is made precise using rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
s. Schilder's theorem is generalized by the Freidlin–Wentzell theorem for Itō diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
s.
Statement of the theorem
Let B be a standard Brownian motion in d-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd starting at the origin, 0 ∈ Rd; let W denote the law
Law (stochastic processes)
In mathematics, the law of a stochastic process is the measure that the process induces on the collection of functions from the index set into the state space...
of B, i.e. classical Wiener measure. For ε > 0, let Wε denote the law of the rescaled process (√ε)B. Then, on the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
C0 = C0([0, T]; Rd) of continuous functions
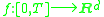such that 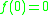, equipped with the supremum norm ||·||∞, the probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s Wε satisfy the large deviations principle with good rate function I : C0 → R ∪ {+∞} given by
if ω is absolutely continuous, and I(ω) = +∞ otherwise. In other words, for every open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
G ⊆ C0 and every closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
F ⊆ C0,
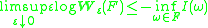
and
Example
Taking ε = 1 ⁄ c2, one can use Schilder's theorem to obtain estimates for the probability that a standard Brownian motion B strays further than c from its starting point over the time interval [0, T], i.e. the probabilityas c tends to infinity. Here Bc(0; ||·||∞) denotes the open ball of radius c about the zero function in C0, taken with respect to the supremum norm. First note that
Since the rate function is continuous on A, Schilder's theorem yields
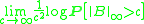
making use of the fact that the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
over paths in the collection A is attained for ω(t) = t ⁄ T. This result can be heuristically interpreted as saying that, for large c and/or large T
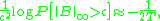
or, in other words,
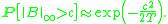
In fact, the above probability can be estimated more precisely as follows: for B a standard Brownian motion in Rn, and any T, c and ε > 0, it holds that