Schatten norm
Encyclopedia
In mathematics
, specifically functional analysis
, the Schatten
norm (or Schatten- Von-Neumann norm)
arises as a generalization of p-integrability similar to the trace class
norm
and the Hilbert–Schmidt norm.
, 
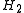be separable Hilbert spaces, and 
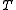a (linear) bounded operator form
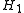to 
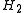. For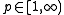 
, define the Schatten p-norm of 
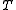as
for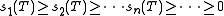
the singular values of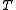
, i.e. the eigenvalues of the Hermitian matrix 
.
From functional calculus
on the positive operator T*T it follows that
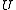and 
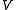unitary operators,
Notice that
is the Hilbert-Schmidt norm (see Hilbert-Schmidt operator) and
is the trace class norm
(see trace class
).
An operator which has a finite Schatten norm is called a Schatten class operator
and the space of such operators is denoted by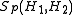
. With this norm, 
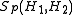is a Banach space, and a Hilbert space for p=2.
Observe that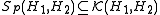
, the algebra of compact operator
s. This follows from the fact that if the sum is finite the spectrum will be finite or countable with the origin as limit point, and hence a compact operator (see compact operator on Hilbert space
).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the Schatten
Robert Schatten
Robert Schatten was a Polish American mathematician.Robert Schatten was born in Lwów. He received his magister degree from Lwów University in 1933. After his emigration to the United States he enrolled at Columbia University and received his master's degree in 1939. He continued his research under...
norm (or Schatten- Von-Neumann norm)
arises as a generalization of p-integrability similar to the trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
and the Hilbert–Schmidt norm.
Definition
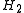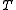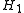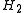Let, be separable Hilbert spaces, and a (linear) bounded operator form to . For 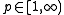, define the Schatten p-norm of 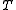as
for
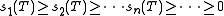
the singular values of
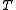, i.e. the eigenvalues of the Hermitian matrix .From functional calculus
Functional calculus
In mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
on the positive operator T*T it follows that
Remarks
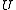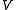The Schatten norm is unitarily invariant: for and unitary operators,
Notice that
is the Hilbert-Schmidt norm (see Hilbert-Schmidt operator) and is the trace class norm(see trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
).
An operator which has a finite Schatten norm is called a Schatten class operator
Schatten class operator
In mathematics, specifically functional analysis, a pth Schatten-class operator is a bounded linear operator on a Hilbert space with finite pth Schatten norm. The space of pth Schatten-class operators is a Banach space with respect to the Schatten norm.Via polar decomposition, one can prove that...
and the space of such operators is denoted by
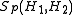. With this norm, 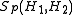is a Banach space, and a Hilbert space for p=2.Observe that
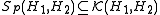, the algebra of compact operatorCompact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s. This follows from the fact that if the sum is finite the spectrum will be finite or countable with the origin as limit point, and hence a compact operator (see compact operator on Hilbert space
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
).