
Scalar-vector-tensor decomposition
Encyclopedia
In cosmological perturbation theory
, the scalar-vector-tensor decomposition is a decomposition of the most general linearized perturbations of the Friedmann-Lemaitre-Robertson-Walker metric into components according to their transformations under spatial rotations. It was first discovered by E. M. Lifshitz in 1946. The general metric perturbation has ten degrees of freedom. The decomposition states that the evolution equations for the most general linearized perturbations of the Friedmann-Lemaitre-Robertson-Walker metric can be decomposed into four scalars, two divergence-free
spatial vector field
s (that is, with a spatial index running from 1 to 3), and a traceless
, symmetric spatial tensor field
with vanishing doubly and singly longitudinal components. The vector and tensor fields each have two independent components, so this decomposition encodes all ten degrees of freedom in the general metric perturbation. Using gauge invariance four of these components (two scalars and a vector field) may be set to zero.
If the perturbed metric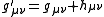 where
where 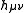 is the perturbation, then the decomposition is as follows,
is the perturbation, then the decomposition is as follows,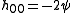
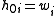
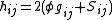
where the Latin indices i and j run over spatial components (1,…,3). The tensor field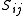 is traceless under the spatial part of the background metric
is traceless under the spatial part of the background metric  (i.e.
(i.e. 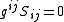 ). The spatial vector
). The spatial vector 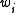 and tensor
and tensor 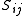 undergo further decomposition. The vector is written
undergo further decomposition. The vector is written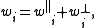
where and
and 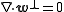 (
(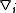 is the covariant derivative
is the covariant derivative
defined with respect to the spatial metric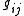 ). The notation is used because in Fourier space, these equations indicate that the vector points parallel and perpendicular to the direction of the wavevector, respectively. The parallel component can be expressed as the gradient of a scalar,
). The notation is used because in Fourier space, these equations indicate that the vector points parallel and perpendicular to the direction of the wavevector, respectively. The parallel component can be expressed as the gradient of a scalar, 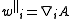 . Thus
. Thus  can be written as a combination of a scalar and a divergenceless, two-component vector.
can be written as a combination of a scalar and a divergenceless, two-component vector.
Finally, an analogous decomposition can be performed on the traceless tensor field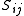 . It can be written
. It can be written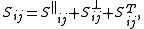
where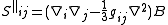 ,
,
where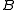 is a scalar (the combination of derivatives is set by the condition that
is a scalar (the combination of derivatives is set by the condition that 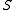 be traceless), and
be traceless), and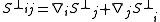 ,
,
where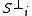 is a divergenceless spatial vector. This leaves only two independent components of
is a divergenceless spatial vector. This leaves only two independent components of 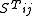 , corresponding to the two polarizations of gravitational wave
, corresponding to the two polarizations of gravitational wave
s. (Since the graviton is massless, the two polarizations are orthogonal to the direction of propagation, just like the photon.)
The advantage of this formulation is that the scalar, vector and tensor evolution equations are decoupled. In representation theory
, this corresponds to decomposing perturbations under the group of spatial rotation
s. Two scalar components and one vector component can further be eliminated by gauge transformations. However, the vector components are generally ignored, as there are few known physical processes in which they can be generated. As indicated above, the tensor components correspond to gravitational waves. The tensor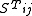 is gauge invariant: it does not change under infinitesimal coordinate transformations.
is gauge invariant: it does not change under infinitesimal coordinate transformations.
Cosmological perturbation theory
In physical cosmology, cosmological perturbation theory is the theory by which the evolution of structure is understood in the big bang model. It uses general relativity to compute the gravitational forces causing small perturbations to grow and eventually seed the formation of stars, quasars,...
, the scalar-vector-tensor decomposition is a decomposition of the most general linearized perturbations of the Friedmann-Lemaitre-Robertson-Walker metric into components according to their transformations under spatial rotations. It was first discovered by E. M. Lifshitz in 1946. The general metric perturbation has ten degrees of freedom. The decomposition states that the evolution equations for the most general linearized perturbations of the Friedmann-Lemaitre-Robertson-Walker metric can be decomposed into four scalars, two divergence-free
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
spatial vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s (that is, with a spatial index running from 1 to 3), and a traceless
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, symmetric spatial tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
with vanishing doubly and singly longitudinal components. The vector and tensor fields each have two independent components, so this decomposition encodes all ten degrees of freedom in the general metric perturbation. Using gauge invariance four of these components (two scalars and a vector field) may be set to zero.
If the perturbed metric
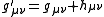 where
where 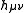 is the perturbation, then the decomposition is as follows,
is the perturbation, then the decomposition is as follows,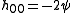
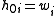
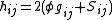
where the Latin indices i and j run over spatial components (1,…,3). The tensor field
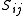 is traceless under the spatial part of the background metric
is traceless under the spatial part of the background metric  (i.e.
(i.e. 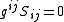 ). The spatial vector
). The spatial vector 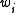 and tensor
and tensor 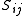 undergo further decomposition. The vector is written
undergo further decomposition. The vector is written
where
 and
and  (
( is the covariant derivative
is the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
defined with respect to the spatial metric
 ). The notation is used because in Fourier space, these equations indicate that the vector points parallel and perpendicular to the direction of the wavevector, respectively. The parallel component can be expressed as the gradient of a scalar,
). The notation is used because in Fourier space, these equations indicate that the vector points parallel and perpendicular to the direction of the wavevector, respectively. The parallel component can be expressed as the gradient of a scalar, 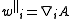 . Thus
. Thus  can be written as a combination of a scalar and a divergenceless, two-component vector.
can be written as a combination of a scalar and a divergenceless, two-component vector.Finally, an analogous decomposition can be performed on the traceless tensor field
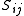 . It can be written
. It can be written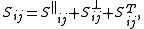
where
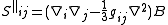 ,
,where
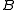 is a scalar (the combination of derivatives is set by the condition that
is a scalar (the combination of derivatives is set by the condition that 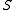 be traceless), and
be traceless), and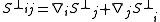 ,
,where
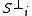 is a divergenceless spatial vector. This leaves only two independent components of
is a divergenceless spatial vector. This leaves only two independent components of 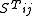 , corresponding to the two polarizations of gravitational wave
, corresponding to the two polarizations of gravitational waveGravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
s. (Since the graviton is massless, the two polarizations are orthogonal to the direction of propagation, just like the photon.)
The advantage of this formulation is that the scalar, vector and tensor evolution equations are decoupled. In representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, this corresponds to decomposing perturbations under the group of spatial rotation
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
s. Two scalar components and one vector component can further be eliminated by gauge transformations. However, the vector components are generally ignored, as there are few known physical processes in which they can be generated. As indicated above, the tensor components correspond to gravitational waves. The tensor
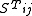 is gauge invariant: it does not change under infinitesimal coordinate transformations.
is gauge invariant: it does not change under infinitesimal coordinate transformations.

