
Axiom S5
Encyclopedia
Axiom S5 is the distinctive axiom
of the S5 modal logic
and states that if possibly p, then necessarily possibly p. It also states, perhaps less intuitively and more controversially, that if possibly necessarily p, then necessarily p. The use of S5 is to eliminate excessive qualifiers (or modal operators) to a proposition, and instead, to accept the final qualifier as the only significant qualifier. That is, S5 discounts all but the final "possibly" or "necessarily."
The axiom is given as either
Both of these axioms are properly called axiom 5.
Basic "Introduction to Modal Logic" books (for example Hughes and Cresswell's, or Brian Chellas') show how this leads in S5 to theorems that can remove all but the last modal operator in a modal stack and get something equivalent to just the last one.
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of the S5 modal logic
S5 (modal logic)
In logic and philosophy, S5 is one of five systems of modal logic proposed byClarence Irving Lewis and Cooper Harold Langford in their 1932 book Symbolic Logic.It is a normal modal logic, and one of the oldest systems of modal logic of any kind....
and states that if possibly p, then necessarily possibly p. It also states, perhaps less intuitively and more controversially, that if possibly necessarily p, then necessarily p. The use of S5 is to eliminate excessive qualifiers (or modal operators) to a proposition, and instead, to accept the final qualifier as the only significant qualifier. That is, S5 discounts all but the final "possibly" or "necessarily."
The axiom is given as either
- Possibly P implies Necessarily Possibly p [
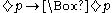 ]
] - Possibly Necessarily P implies Necessarily p [
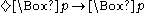 ]
]
Both of these axioms are properly called axiom 5.
Basic "Introduction to Modal Logic" books (for example Hughes and Cresswell's, or Brian Chellas') show how this leads in S5 to theorems that can remove all but the last modal operator in a modal stack and get something equivalent to just the last one.
External links
- http://home.utah.edu/~nahaj/logic/structures/axioms/CMpLMp.html
- http://plato.stanford.edu/entries/logic-modal/

