In complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, Runge's theorem, also known as Runge's approximation theorem, named after the German Mathematician Carl Runge, and put forward by him in the year 1885, states the following: If K is a compact subset of C (the set of complex numbers), A is a set containing at least one complex number from every bounded

Bounded set

In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...

 connected component of C\K, and f is a holomorphic function

Holomorphic function

In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...

 on an open set containing K, then there exists a sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

  of rational function

Rational function

In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...

s all of whose poles are in A such that the sequence approaches the function f uniformly on K.

Note that not every complex number in A need be a pole of every rational function of the sequence 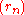. We merely know that if some 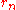of the sequence has poles, those poles are in A.

One of the things that makes this theorem so powerful is that one can choose the set A at will. In other words, one can pick any complex numbers as one wishes from the bounded connected components of C\K. Then the theorem guarantees the existence of a sequence of rational functions with poles only in those chosen numbers.

In the special case that C\K is a connected set, the set A in the theorem will clearly be empty. And since rational functions with no poles are indeed nothing but polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

s, we get the following corollary

Corollary

A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...

: If K is a compact subset of C such that C\K is a connected set, and f is a holomorphic function on K, then there exists a sequence of polynomials 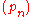that approaches f uniformly on K.

A slightly more general version of this theorem is obtained if one takes A to be a subset of the Riemann sphere

Riemann sphere

In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...

C∪{∞} and then requires A to intersect also the unbounded connected component of K (which now contains ∞). That is, in the formulation given above, the rational functions may turn out to have a pole at infinity, while in the more general formulation the pole can be chosen instead anywhere in the unbounded connected component of K.