Runge's phenomenon
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
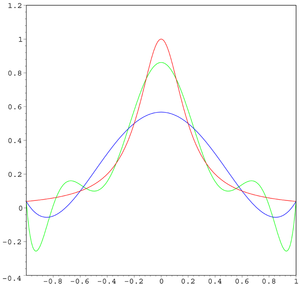
, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
with polynomials of high degree. It was discovered by Carl David Tolmé Runge when exploring the behavior of errors when using polynomial interpolation to approximate certain functions.
The discovery was important because it shows that going to higher degrees does not always improve accuracy. The phenomenon is similar to the Gibbs phenomenon
Gibbs phenomenon
In mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
in Fourier series approximations.
Introduction
The Weierstrass approximation theorem states that every continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
f(x) defined on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a,b] can be uniformly approximated as closely as desired by a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function Pn(x) of degree ≤ n, i.e.,
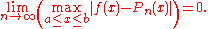
Interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
at equidistant points is a natural and well-known approach to construct approximating polynomials.
Runge's phenomenon demonstrates, however, that interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
can easily result in divergent approximations.
Problem
Consider the functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
:
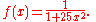
Runge found that if this function is interpolated
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
at equidistant points xi between −1 and 1 such that:
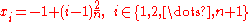
with a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
Pn(x) of degree ≤ n, the resulting interpolation oscillates toward the end of the interval, i.e. close to −1 and 1. It can even be proven that the interpolation error tends toward infinity when the degree of the polynomial increases:
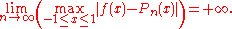
This shows that high-degree polynomial interpolation at equidistant points can be troublesome.
Reason
The error between the generating function and the interpolating polynomial of order n is given by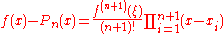
for some
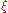in (−1, 1). Thus,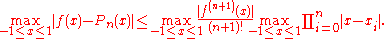
For the case of the Runge function, interpolated at equidistant points,
each of the two multipliers in the upper bound for the approximation error grows to infinity with n.
Although often used to explain the Runge phenomenon, the fact that the upper bound of the error goes to infinity does not necessarily
imply, of course, that the error itself also diverges with n.
Change of interpolation points
The oscillation can be minimized by using nodes that are distributed more densely towards the edges of the interval, specifically, with asymptotic density (on the interval [−1,1]) given by the formula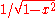
.A standard example of such a set of nodes is Chebyshev nodes
Chebyshev nodes
In numerical analysis, Chebyshev nodes are the roots of the Chebyshev polynomial of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the Runge's phenomenon.-Definition:...
, for which the maximum error in approximating the Runge function is guaranteed to diminish with increasing polynomial order. The phenomenon demonstrates that high degree polynomials are generally unsuitable for interpolation with equidistant nodes.
Use of piecewise polynomials
The problem can be avoided by using spline curves which are piecewise polynomials. When trying to decrease the interpolation error one can increase the number of polynomial pieces which are used to construct the spline instead of increasing the degree of the polynomials used.Constrained minimization
One can also fit a polynomial of higher degree (for instance
instead of 
), and fit an interpolating polynomial whose first (or second) derivative has minimal 
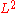norm.Least squares fitting
Another method is fitting a polynomial of lower degree using the method of least squaresLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
. Generally, when using m equidistant points, if
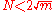then least squares approximation 
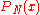is well-conditioned.Related statements from the approximation theoryApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
For every predefined table of interpolation nodes there is a continuous function for which the interpolation process on those nodes diverges. For every continuous function there is a table of nodes on which the interpolation process converges. Chebyshev interpolation (i.e., on Chebyshev nodesChebyshev nodes
In numerical analysis, Chebyshev nodes are the roots of the Chebyshev polynomial of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the Runge's phenomenon.-Definition:...
) converges uniformly for every absolutely continuous function.
See also
- Compare with the Gibbs phenomenonGibbs phenomenonIn mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
for sinusoidal basis functions - Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
- Chebyshev nodesChebyshev nodesIn numerical analysis, Chebyshev nodes are the roots of the Chebyshev polynomial of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the Runge's phenomenon.-Definition:...
- Stone–Weierstrass theorem