
Risk dominance
Encyclopedia
Risk dominance and payoff dominance are two related refinements of the Nash equilibrium
(NE) solution concept
in game theory
, defined by John Harsanyi
and Reinhard Selten
. A Nash equilibrium is considered payoff dominant if it is Pareto superior
to all other Nash equilibria in the game. When faced with a choice among equilibria, all players would agree on the payoff dominant equilibrium since it offers to each player at least as much payoff as the other Nash equilibria. Conversely, a Nash equilibrium is considered risk dominant if it has the largest basin of attraction, meaning the more uncertainty players have about the actions of the other player(s), the more likely they will choose the strategy corresponding to it.
The payoff matrix in Figure 1 provides a simple two-player, two-strategy example of a game with two pure Nash equilibria. The strategy pair (Hunt, Hunt) is payoff dominant since payoffs are higher for both players compared to the other pure NE, (Gather, Gather). On the other hand, (Gather, Gather) risk dominates (Hunt, Hunt) since if uncertainty exists about the other player's action, gathering will provide a higher expected payoff. The game in Figure 1 is a well-known game-theoretic dilemma called stag hunt
. The rationale behind it is that communal action (hunting) yields a higher return if all players combine their skills, but if it is unknown whether the other player helps in hunting, gathering might turn out to be the better individual strategy for food provision, since it does not depend on coordinating
with the other player. In addition, gathering alone is preferred to gathering in competition with others. Like the Prisoner's dilemma
, it provides a reason why collective action
might fail in the absence of credible commitments.
if the following payoff inequalities hold for player 1 (rows): A > B, D > C, and for player 2 (columns): a > b, d > c. The strategy pairs (H, H) and (G, G) are then the only pure Nash equilibria. In addition there is a mixed Nash equilibrium where player 1 plays H with probability p = (d-c)/(a-b-c+d) and G with probability 1–p; player 2 plays H with probability q = (D-C)/(A-B-C+D) and G with probability 1–q.
Strategy pair (H, H) payoff dominates (G, G) if A ≥ D, a ≥ d, and at least one of the two is a strict inequality: A > D or a > d.
Strategy pair (G, G) risk dominates (H, H) if the product of the deviation losses is highest for (G, G) (Harsanyi and Selten, 1988, Lemma 5.4.4). In other words, if the following inequality holds: . If the inequality is strict then (G, G) strictly risk dominates (H, H).(That is, players have more incentive to deviate).
If the game is symmetric, so if A = a, B = b, etc., the inequality allows for a simple interpretation: We assume the players are unsure about which strategy the opponent will pick and assign probabilities for each strategy. If each player assigns probabilities ½ to H and G each, then (G, G) risk dominates (H, H) if the expected payoff from playing G exceeds the expected payoff from playing H: , or simply .
Another way to calculate the risk dominant equilibrium is to calculate the risk factor for all equilibria and to find the equilibrium with the smallest risk factor. To calculate the risk factor in our 2x2 game, consider the expected payoff to a player if they play H: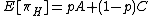 (where p is the probability that the other player will play H), and compare it to the expected payoff if they play G:
(where p is the probability that the other player will play H), and compare it to the expected payoff if they play G: 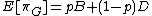 . The value of p which makes these two expected values equal is the risk factor for the equilibrium (H, H), with
. The value of p which makes these two expected values equal is the risk factor for the equilibrium (H, H), with 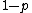 the risk factor for playing (G, G). You can also calculate the risk factor for playing (G, G) by doing the same calculation, but setting p as the probability the other player will play G. An interpretation for p is it is the smallest probability that the opponent will play a strategy such that the payoff of that strategy is greater than if the other strategy was played.
the risk factor for playing (G, G). You can also calculate the risk factor for playing (G, G) by doing the same calculation, but setting p as the probability the other player will play G. An interpretation for p is it is the smallest probability that the opponent will play a strategy such that the payoff of that strategy is greater than if the other strategy was played.
, predicts that the risk dominant state is the only stochastically stable equilibrium. Both models assume that multiple two-player games are played in a population of N players. The players are matched randomly with opponents, with each player having equal likelihoods of drawing any of the N−1 other players. The players start with a pure strategy, G or H, and play this strategy against their opponent. In replicator dynamics, the population game is repeated in sequential generations where subpopulations change based on the success of their chosen stratregies. In best response, players update their strategies to improve expected payoffs in the subsequent generations. The recognition of Kandori, Mailath & Rob (1993) and Young (1993) was that if the rule to update one's strategy allows for mutation, and the probability of mutation vanishes, i.e. asymptotically reaches zero over time, the likelihood that the risk dominant equilibrium is reached goes to one, even if it is payoff dominated.
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
(NE) solution concept
Solution concept
In game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
in game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, defined by John Harsanyi
John Harsanyi
John Charles Harsanyi was a Hungarian-Australian-American economist and Nobel Memorial Prize in Economic Sciences winner....
and Reinhard Selten
Reinhard Selten
-Life and career:Selten was born in Breslau in Lower Silesia, now in Poland, to a Jewish father, Adolf Selten, and Protestant mother, Käthe Luther. For his work in game theory, Selten won the 1994 Nobel Memorial Prize in Economic Sciences...
. A Nash equilibrium is considered payoff dominant if it is Pareto superior
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
to all other Nash equilibria in the game. When faced with a choice among equilibria, all players would agree on the payoff dominant equilibrium since it offers to each player at least as much payoff as the other Nash equilibria. Conversely, a Nash equilibrium is considered risk dominant if it has the largest basin of attraction, meaning the more uncertainty players have about the actions of the other player(s), the more likely they will choose the strategy corresponding to it.
The payoff matrix in Figure 1 provides a simple two-player, two-strategy example of a game with two pure Nash equilibria. The strategy pair (Hunt, Hunt) is payoff dominant since payoffs are higher for both players compared to the other pure NE, (Gather, Gather). On the other hand, (Gather, Gather) risk dominates (Hunt, Hunt) since if uncertainty exists about the other player's action, gathering will provide a higher expected payoff. The game in Figure 1 is a well-known game-theoretic dilemma called stag hunt
Stag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
. The rationale behind it is that communal action (hunting) yields a higher return if all players combine their skills, but if it is unknown whether the other player helps in hunting, gathering might turn out to be the better individual strategy for food provision, since it does not depend on coordinating
Coordination game
In game theory, coordination games are a class of games with multiple pure strategy Nash equilibria in which players choose the same or corresponding strategies...
with the other player. In addition, gathering alone is preferred to gathering in competition with others. Like the Prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
, it provides a reason why collective action
Collective action
Collective action is the pursuit of a goal or set of goals by more than one person. It is a term which has formulations and theories in many areas of the social sciences.-In sociology:...
might fail in the absence of credible commitments.
Formal definition
The game given in Figure 2 is a coordination gameCoordination game
In game theory, coordination games are a class of games with multiple pure strategy Nash equilibria in which players choose the same or corresponding strategies...
if the following payoff inequalities hold for player 1 (rows): A > B, D > C, and for player 2 (columns): a > b, d > c. The strategy pairs (H, H) and (G, G) are then the only pure Nash equilibria. In addition there is a mixed Nash equilibrium where player 1 plays H with probability p = (d-c)/(a-b-c+d) and G with probability 1–p; player 2 plays H with probability q = (D-C)/(A-B-C+D) and G with probability 1–q.
Strategy pair (H, H) payoff dominates (G, G) if A ≥ D, a ≥ d, and at least one of the two is a strict inequality: A > D or a > d.
Strategy pair (G, G) risk dominates (H, H) if the product of the deviation losses is highest for (G, G) (Harsanyi and Selten, 1988, Lemma 5.4.4). In other words, if the following inequality holds: . If the inequality is strict then (G, G) strictly risk dominates (H, H).(That is, players have more incentive to deviate).
If the game is symmetric, so if A = a, B = b, etc., the inequality allows for a simple interpretation: We assume the players are unsure about which strategy the opponent will pick and assign probabilities for each strategy. If each player assigns probabilities ½ to H and G each, then (G, G) risk dominates (H, H) if the expected payoff from playing G exceeds the expected payoff from playing H: , or simply .
Another way to calculate the risk dominant equilibrium is to calculate the risk factor for all equilibria and to find the equilibrium with the smallest risk factor. To calculate the risk factor in our 2x2 game, consider the expected payoff to a player if they play H:
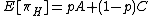 (where p is the probability that the other player will play H), and compare it to the expected payoff if they play G:
(where p is the probability that the other player will play H), and compare it to the expected payoff if they play G: 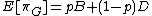 . The value of p which makes these two expected values equal is the risk factor for the equilibrium (H, H), with
. The value of p which makes these two expected values equal is the risk factor for the equilibrium (H, H), with 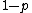 the risk factor for playing (G, G). You can also calculate the risk factor for playing (G, G) by doing the same calculation, but setting p as the probability the other player will play G. An interpretation for p is it is the smallest probability that the opponent will play a strategy such that the payoff of that strategy is greater than if the other strategy was played.
the risk factor for playing (G, G). You can also calculate the risk factor for playing (G, G) by doing the same calculation, but setting p as the probability the other player will play G. An interpretation for p is it is the smallest probability that the opponent will play a strategy such that the payoff of that strategy is greater than if the other strategy was played.Equilibrium selection
A number of evolutionary approaches have established that when played in a large population, players might fail to play the payoff dominant equilibrium strategy and instead end up in the payoff dominated, risk dominant equilibrium. Two separate evolutionary models both support the idea that the risk dominant equilibrium is more likely to occur. The first model, based on replicator dynamics, predicts that a population is more likely to adopt the risk dominant equilibrium than the payoff dominant equilibrium. The second model, based on best response strategy revision and mutationMutation
In molecular biology and genetics, mutations are changes in a genomic sequence: the DNA sequence of a cell's genome or the DNA or RNA sequence of a virus. They can be defined as sudden and spontaneous changes in the cell. Mutations are caused by radiation, viruses, transposons and mutagenic...
, predicts that the risk dominant state is the only stochastically stable equilibrium. Both models assume that multiple two-player games are played in a population of N players. The players are matched randomly with opponents, with each player having equal likelihoods of drawing any of the N−1 other players. The players start with a pure strategy, G or H, and play this strategy against their opponent. In replicator dynamics, the population game is repeated in sequential generations where subpopulations change based on the success of their chosen stratregies. In best response, players update their strategies to improve expected payoffs in the subsequent generations. The recognition of Kandori, Mailath & Rob (1993) and Young (1993) was that if the rule to update one's strategy allows for mutation, and the probability of mutation vanishes, i.e. asymptotically reaches zero over time, the likelihood that the risk dominant equilibrium is reached goes to one, even if it is payoff dominated.

