
Retkes convergence criterion
Encyclopedia
In mathematics, the Retkes convergence criterion, named after Zoltán Retkes, gives necessary and sufficient conditions for convergence of numerical series
. Numerous criteria are known for testing convergence. The most famous of them is the so called Cauchy criterion, the only one that gives necessary and sufficient conditions. Under weak restrictions the Retkes criterion gave a new necessary and sufficient condition for the convergence. The criterion will be formulated in the complex settings:
Assume that and
and  if
if  . Then
. Then
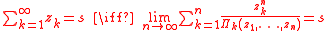
In the above formula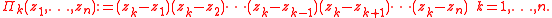
The equivalence can be proved by using the Hermite–Hadamard inequality.
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. Numerous criteria are known for testing convergence. The most famous of them is the so called Cauchy criterion, the only one that gives necessary and sufficient conditions. Under weak restrictions the Retkes criterion gave a new necessary and sufficient condition for the convergence. The criterion will be formulated in the complex settings:
Assume that
 and
and  if
if  . Then
. Then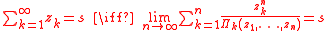
In the above formula
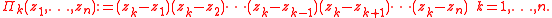
The equivalence can be proved by using the Hermite–Hadamard inequality.

