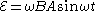
Related rates
Encyclopedia
In differential calculus
, related rates problems involve finding a rate at which a quantity changes by relating
that quantity to other quantities whose rates of change are known. The rate of change is usually with respect to time
. Because science and engineering often relate quantities to each other, the methods of related rates have broad applications in these fields. Because problems to which related rate methods apply often have nested functions, solving these problems often requires application of the chain rule
.
Errors in this procedure are often caused by plugging in the known values for the variables before (rather than after) finding the derivative with respect to time. Doing so will yield an incorrect result, since if you plug in the values for the variables, those variables will become constants; and when you differentiate the equation, you will end up with zeroes in places of all variables for which you plugged in the values.
The distance between the base of the ladder and the wall, x, and the height of the ladder on the wall, y, represent the sides of a right triangle
with the ladder as the hypotenuse, h. The object is to find dy/dt, the rate of change of y with respect to time, t, when h, x and dx/dt, the rate of change of x, are known.
Step 1: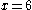
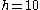
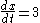
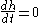
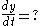
Step 2:
From the Pythagorean theorem
, the equation ,
,
describes the relationship between x, y and h, for a right triangle. Differentiating both sides of this equation with respect to time, t, yields
Step 3:
When solved for the wanted rate of change, dy/dt, gives us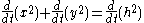

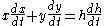
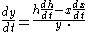
Step 4 & 5:
Using the variables from step 1 gives us: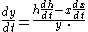
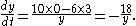
Solving for y using the Pythagorean Theorem gives:
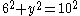

Plugging in 8 for the equation: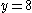
It is generally assumed that negative values represent the downward direction. In doing such, the top of the ladder is sliding down the wall at a rate of meters per second.
and electromagnetic induction
.
Big idea: use chain rule to compute rate of change of distance between two vehicles.
Plan:
Choose coordinate system:
Let the y-axis point North and the x-axis point East.
Identify variables:
Define y(t) to be the distance of the vehicle heading North from the origin and x(t) to be the distance of the vehicle heading West from the origin.
Express c in terms of x and y via Pythagorean theorem:
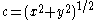
Express dc/dt using chain rule in terms of dx/dt and dy/dt:
Substitute in x = 4 mi, y = 3 mi, dx/dt = -80 mi/hr, dy/dt = 60 mi/hr and Simplify
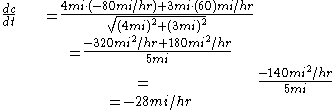
Consequently, the two vehicles are getting closer together at a rate of 28 mi/hr.
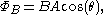
Faraday's law
of electromagnetic induction states that the induced electromotive force
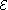 is the negative rate of change of magnetic flux
is the negative rate of change of magnetic flux 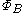 through a conducting loop.
through a conducting loop.

If the loop area A and magnetic field B are held constant, but the loop is rotated so that the angle θ is a known function of time, the rate of change of θ can be related to the rate of change of (and therefore the electromotive force) by taking the time derivative of the flux relation
(and therefore the electromotive force) by taking the time derivative of the flux relation

If for example, the loop is rotating at a constant angular velocity ω, so that θ=ωt, then
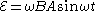
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, related rates problems involve finding a rate at which a quantity changes by relating
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
that quantity to other quantities whose rates of change are known. The rate of change is usually with respect to time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
. Because science and engineering often relate quantities to each other, the methods of related rates have broad applications in these fields. Because problems to which related rate methods apply often have nested functions, solving these problems often requires application of the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
.
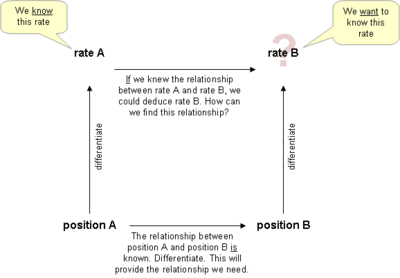
Procedure
The most common way to approach related rates problems is the following:- Identify the known variablesVariable (mathematics)In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, including rates of change and the rate of change that is to be found. (Drawing a picture or representation of the problem can help to keep everything in order) - Construct an equationEquationAn equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
relating the quantities whose rates of change are known to the quantity whose rate of change is to be found. - DifferentiateDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
both sides of the equation with respect to time (or other rate of change). Often, the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
is employed at this step. - Substitute the known rates of change and the known quantities into the equation.
- Solve for the wanted rate of change.
Errors in this procedure are often caused by plugging in the known values for the variables before (rather than after) finding the derivative with respect to time. Doing so will yield an incorrect result, since if you plug in the values for the variables, those variables will become constants; and when you differentiate the equation, you will end up with zeroes in places of all variables for which you plugged in the values.

Leaning ladder example
A 10-meter ladder is leaning against the wall of a building, and the base of the ladder is sliding away from the building at a rate of 3 meters per second. How fast is the top of the ladder sliding down the wall when the base of the ladder is 6 meters from the wall?The distance between the base of the ladder and the wall, x, and the height of the ladder on the wall, y, represent the sides of a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
with the ladder as the hypotenuse, h. The object is to find dy/dt, the rate of change of y with respect to time, t, when h, x and dx/dt, the rate of change of x, are known.
Step 1:
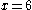
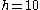
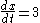
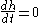
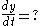
Step 2:
From the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, the equation
 ,
,describes the relationship between x, y and h, for a right triangle. Differentiating both sides of this equation with respect to time, t, yields

Step 3:
When solved for the wanted rate of change, dy/dt, gives us
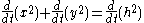

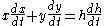
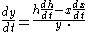
Step 4 & 5:
Using the variables from step 1 gives us:
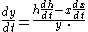
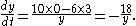
Solving for y using the Pythagorean Theorem gives:

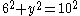

Plugging in 8 for the equation:
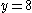
It is generally assumed that negative values represent the downward direction. In doing such, the top of the ladder is sliding down the wall at a rate of meters per second.
Physics Examples
Because one physical quantity often depends on another, which, in turn depends on others, such as time, related rate methods have broad applications in Physics. This section presents an example of related rates kinematicsKinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
and electromagnetic induction
Electromagnetic induction
Electromagnetic induction is the production of an electric current across a conductor moving through a magnetic field. It underlies the operation of generators, transformers, induction motors, electric motors, synchronous motors, and solenoids....
.
Physics Example I: Relative Kinematics of Two Vehicles
For example, one can consider the kinematics problem where one vehicle is heading West toward an intersection at 80 miles per hour while another is heading North away from the intersection at 60 miles per hour. One can ask whether the vehicles are getting closer or further apart and at what rate at the moment when the North bound vehicle is 3 miles North of the intersection and the West bound vehicle is 4 miles East of the intersection.Big idea: use chain rule to compute rate of change of distance between two vehicles.
Plan:
- Choose coordinate system
- Identify variables
- Draw picture
- Big idea: use chain rule to compute rate of change of distance between two vehicles
- Express c in terms of x and y via Pythagorean theorem
- Express dc/dt using chain rule in terms of dx/dt and dy/dt
- Substitute in x, y, dx/dt, dy/dt
- Simplify.
Choose coordinate system:
Let the y-axis point North and the x-axis point East.
Identify variables:
Define y(t) to be the distance of the vehicle heading North from the origin and x(t) to be the distance of the vehicle heading West from the origin.
Express c in terms of x and y via Pythagorean theorem:
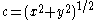
Express dc/dt using chain rule in terms of dx/dt and dy/dt:
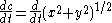 |
Apply derivative operator to entire function |
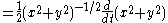 |
Square root is outside function; Sum of squares is inside function |
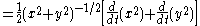 |
Distribute differentiation operator |
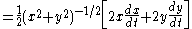 |
Apply chain rule to x(t) and y(t)} |
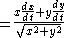 |
Simplify. |
Substitute in x = 4 mi, y = 3 mi, dx/dt = -80 mi/hr, dy/dt = 60 mi/hr and Simplify
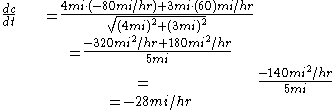
Consequently, the two vehicles are getting closer together at a rate of 28 mi/hr.
Physics Example II: Electromagnetic induction of conducting loop spinning in magnetic field
The magnetic flux through a loop of area A whose normal is at an angle θ to a magnetic field of strength B is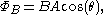
Faraday's law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
of electromagnetic induction states that the induced electromotive force
Electromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
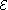 is the negative rate of change of magnetic flux
is the negative rate of change of magnetic flux 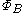 through a conducting loop.
through a conducting loop.
If the loop area A and magnetic field B are held constant, but the loop is rotated so that the angle θ is a known function of time, the rate of change of θ can be related to the rate of change of
 (and therefore the electromotive force) by taking the time derivative of the flux relation
(and therefore the electromotive force) by taking the time derivative of the flux relation
If for example, the loop is rotating at a constant angular velocity ω, so that θ=ωt, then