
Regular semi-algebraic system
Encyclopedia
In computer algebra, a regular semi-algebraic system is a particular kind of triangular system of multivariate polynomials over a real closed field.
s and triangular decomposition
s are fundamental and well-developed tools for describing the complex solutions of polynomial systems. The notion of a regular semi-algebraic system is an adaptation of the concept of a regular chain focusing on solutions of the real analogue: semi-algebraic systems.
Any semi-algebraic system can be decomposed into finitely many regular semi-algebraic systems
can be decomposed into finitely many regular semi-algebraic systems  such that a point (with real coordinates) is a solution of
such that a point (with real coordinates) is a solution of  if and only if it is a solution of one of the systems
if and only if it is a solution of one of the systems  .
.
 be a regular chain
be a regular chain
of
for some ordering of the variables and a real closed field
and a real closed field
 .
.
Let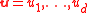 and
and 
designate respectively the variables of that are free and algebraic with respect to
that are free and algebraic with respect to  . Let
. Let  be finite such that
be finite such that
each polynomial in is regular w.r.t.\ the saturated ideal of
is regular w.r.t.\ the saturated ideal of  .
.
Define . Let
. Let  be a quantifier-free
be a quantifier-free
formula of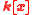 involving only the variables of
involving only the variables of  . We say that
. We say that 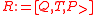 is a regular semi-algebraic system if the following three conditions hold.
is a regular semi-algebraic system if the following three conditions hold.
The zero set of , denoted by
, denoted by 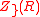 ,
,
is defined as the set of points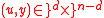 such that
such that 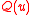 is true and
is true and 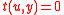 ,
, 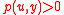 , for all
, for all 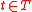 and all
and all 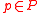 .
.
Introduction
Regular chainRegular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
s and triangular decomposition
Triangular decomposition
In computer algebra, a triangular decomposition of a polynomial system S is a set of simpler polynomial systems S_1,\ldots, S_e such that a point is a solution of S if and only if it is a solution of one of the systems S_1,\ldots, S_e....
s are fundamental and well-developed tools for describing the complex solutions of polynomial systems. The notion of a regular semi-algebraic system is an adaptation of the concept of a regular chain focusing on solutions of the real analogue: semi-algebraic systems.
Any semi-algebraic system
 can be decomposed into finitely many regular semi-algebraic systems
can be decomposed into finitely many regular semi-algebraic systems  such that a point (with real coordinates) is a solution of
such that a point (with real coordinates) is a solution of  if and only if it is a solution of one of the systems
if and only if it is a solution of one of the systems  .
.Formal definition
Let be a regular chain
be a regular chainRegular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
of

for some ordering of the variables
 and a real closed field
and a real closed fieldReal closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
 .
.Let
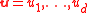 and
and 
designate respectively the variables of
 that are free and algebraic with respect to
that are free and algebraic with respect to  . Let
. Let  be finite such that
be finite such thateach polynomial in
 is regular w.r.t.\ the saturated ideal of
is regular w.r.t.\ the saturated ideal of  .
.Define
 . Let
. Let  be a quantifier-free
be a quantifier-freeformula of
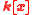 involving only the variables of
involving only the variables of  . We say that
. We say that 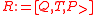 is a regular semi-algebraic system if the following three conditions hold.
is a regular semi-algebraic system if the following three conditions hold.-
 defines a non-empty open semi-algebraic set
defines a non-empty open semi-algebraic set 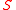 of
of 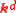 ,
, - the regular system
 specializes well at every point
specializes well at every point  of
of  ,
, - at each point
 of
of 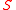 , the specialized system
, the specialized system 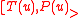 has at least one real zero.
has at least one real zero.
The zero set of
 , denoted by
, denoted by 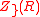 ,
,is defined as the set of points
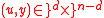 such that
such that 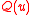 is true and
is true and 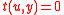 ,
, 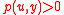 , for all
, for all 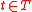 and all
and all 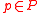 .
.See also
- Characteristic setCharacteristic setWenjun Wu's method is an algorithm for solving multivariate polynomial equations introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt...
- Triangular decompositionTriangular decompositionIn computer algebra, a triangular decomposition of a polynomial system S is a set of simpler polynomial systems S_1,\ldots, S_e such that a point is a solution of S if and only if it is a solution of one of the systems S_1,\ldots, S_e....
- Regular chainRegular chainIn computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
- RegularChainsRegularChainsThe RegularChains package in the computer algebra software package Maple is a collection of commands for solving systems of polynomial equations, inequations and inequalities symbolically....
- Real algebraic geometryReal algebraic geometryIn mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....

