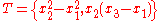Regular chain
Encyclopedia
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set
.
. For the non-linear case,
given a polynomial system F over a field, one can convert (decompose or triangularize) it to a finite set of triangular sets, in the sense that the algebraic variety
V(F) is described by these triangular sets.
A triangular set may merely describe the empty set. To fix this degenerated case, the notion of regular chain was introduced, independently by Kalkbrener (1993), Yang and Zhang (1994). Regular chains also appear in Chou and Gao (1992). Regular chains are special triangular sets which are used in different algorithms for computing unmixed-dimensional decompositions of algebraic varieties. Without using factorization, these decompositions have better properties that the ones produced by Wu's algorithm. Kalkbrener's original definition was based on the following observation: every irreducible variety is uniquely determined by one of its generic point
s and varieties can be represented by describing the generic points of their irreducible components. These generic points are given by regular chains.
is a triangular set and also a regular chain. Two generic points given by T are (a, a, a) and (a, -a, a) where a is transcendental over Q.
Thus there are two irreducible components, given by { x2 - x1, x3 - x1 } and { x2 + x1, x3 - x1 }, respectively.
Note that: (1) the content
of the second polynomial is x2, which does not contribute to the generic points represented and thus can be removed; (2) the dimension
of each component is 1, the number of free variables in the regular chain.
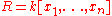
are always sorted as x1 < ... < xn.
A non-constant polynomial f in
can be seen as a univariate polynomial in its greatest variable.
The greatest variable in f is called its main variable, denoted by mvar(f). Let u be
the main variable of f and write it as
,
where e is the degree of f w.r.t. u and
is
the leading coefficient of f w.r.t. u. Then the initial of f
is
and e is its main degree.
A non-empty subset T of
is a triangular set,
if the polynomials in T are non-constant and have distinct main variables.
Hence, a triangular set is finite, and has cardinality at most n.
Let T = {t1, ..., ts} be a triangular set such that
mvar(t1) < ... < mvar(ts),
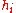be the initial of ti and h be the product of hi's.
Then T is a regular chain if
Characteristic set
Wenjun Wu's method is an algorithm for solving multivariate polynomial equations introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt...
.
Introduction
Given a linear system, one can convert it to a triangular system via Gaussian eliminationGaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
. For the non-linear case,
given a polynomial system F over a field, one can convert (decompose or triangularize) it to a finite set of triangular sets, in the sense that the algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V(F) is described by these triangular sets.
A triangular set may merely describe the empty set. To fix this degenerated case, the notion of regular chain was introduced, independently by Kalkbrener (1993), Yang and Zhang (1994). Regular chains also appear in Chou and Gao (1992). Regular chains are special triangular sets which are used in different algorithms for computing unmixed-dimensional decompositions of algebraic varieties. Without using factorization, these decompositions have better properties that the ones produced by Wu's algorithm. Kalkbrener's original definition was based on the following observation: every irreducible variety is uniquely determined by one of its generic point
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
s and varieties can be represented by describing the generic points of their irreducible components. These generic points are given by regular chains.
Examples
Denote Q the rational number field. In Q[x1, x2, x3] with variable ordering x1 < x2 < x3,
is a triangular set and also a regular chain. Two generic points given by T are (a, a, a) and (a, -a, a) where a is transcendental over Q.
Thus there are two irreducible components, given by { x2 - x1, x3 - x1 } and { x2 + x1, x3 - x1 }, respectively.
Note that: (1) the content
Content (algebra)
In algebra, the content of a polynomial is the highest common factor of its coefficients.A polynomial is primitive if it has content unity....
of the second polynomial is x2, which does not contribute to the generic points represented and thus can be removed; (2) the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of each component is 1, the number of free variables in the regular chain.
Formal definitions
The variables in the polynomial ring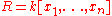are always sorted as x1 < ... < xn.
A non-constant polynomial f in
can be seen as a univariate polynomial in its greatest variable.The greatest variable in f is called its main variable, denoted by mvar(f). Let u be
the main variable of f and write it as
,where e is the degree of f w.r.t. u and
isthe leading coefficient of f w.r.t. u. Then the initial of f
is
and e is its main degree.- Triangular set
A non-empty subset T of
is a triangular set,if the polynomials in T are non-constant and have distinct main variables.
Hence, a triangular set is finite, and has cardinality at most n.
- Regular chain
Let T = {t1, ..., ts} be a triangular set such that
mvar(t1) < ... < mvar(ts),
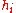be the initial of ti and h be the product of hi's.Then T is a regular chain if
-
,
where each resultant is computed with respect to the main variable of ti, respectively.
This definition is from Yang and Zhang, which is of much algorithmic flavor.
- Quasi-component and saturated ideal of a regular chain
The quasi-component W(T) described by the regular chain T is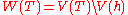
, that is,
the set difference of the varieties V(T) and V(h).
The attached algebraic object of a regular chain is its saturated ideal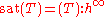
.
A classic result is that the Zariski closure of W(T) equals the variety defined by sat(T), that is,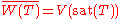
,
and its dimension is n - |T|, the difference of the number of variables and the number of polynomials in T.
- Triangular decompositions
In general, there are two ways to decompose a polynomial system F. The first one is to decompose lazily, that is, only to represent its generic pointGeneric pointIn mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
s in the (Kalkbrener) sense,-
.
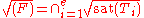The second is to describe all zeroes in the (Lazard) sense,-
.
There are various algorithms available for triangular decompositions in either sense.
Properties
Let T be a regular chain in the polynomial ring R.
- The saturated ideal sat(T) is an unmixed ideal with dimension n − |T|.
- A regular chain holds a strong elimination property in the sense that:
-
.
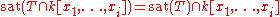- A polynomial p is in sat(T) if and only if p is pseudo-reduced to zero by T, that is,
-
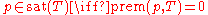. - Hence the membership test for sat(T) is algorithmic.
- A polynomial p is a zero-divisor modulo sat(T) if and only if
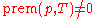and 
.
- Hence the regularity test for sat(T) is algorithmic.
- Given a prime ideal P, there exists a regular chain C such that P = sat(C).
- If the first element of a regular chain C is an irreducible polynomial and the others are linear in their main variable, then sat(C) is a prime ideal.
- Conversely, if P is a prime ideal, then, after almost all linear changes of variables, there exists a regular chain C of the preceding shape such that P = sat(C).
- A triangular set is a regular chain if and only if it is a Ritt characteristic setCharacteristic setWenjun Wu's method is an algorithm for solving multivariate polynomial equations introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt...
of its saturated ideal.
See also
- Characteristic setCharacteristic setWenjun Wu's method is an algorithm for solving multivariate polynomial equations introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt...
- Groebner basis
- RegularChainsRegularChainsThe RegularChains package in the computer algebra software package Maple is a collection of commands for solving systems of polynomial equations, inequations and inequalities symbolically....
- Regular semi-algebraic systemRegular semi-algebraic systemIn computer algebra, a regular semi-algebraic system is a particular kind of triangular system of multivariate polynomials over a real closed field.- Introduction :...
- Triangular decompositionTriangular decompositionIn computer algebra, a triangular decomposition of a polynomial system S is a set of simpler polynomial systems S_1,\ldots, S_e such that a point is a solution of S if and only if it is a solution of one of the systems S_1,\ldots, S_e....
Further references
- P. Aubry, D. Lazard, M. Moreno Maza. On the theories of triangular sets. Journal of Symbolic Computation, 28(1–2):105–124, 1999.
- F. Boulier and F. Lemaire and M. Moreno Maza. Well known theorems on triangular systems and the D5 principle. Transgressive Computing 2006, Granada, Spain.
- E. Hubert. Notes on triangular sets and triangulation-decomposition algorithms I: Polynomial systems. LNCS, volume 2630, Springer-Verlag Heidelberg.
- F. Lemaire and M. Moreno Maza and Y. Xie. The RegularChains library. Maple Conference 2005.
- M. Kalkbrener: Algorithmic Properties of Polynomial Rings. J. Symb. Comput. 26(5): 525–581 (1998).
- M. Kalkbrener: A Generalized Euclidean Algorithm for Computing Triangular Representations of Algebraic Varieties. J. Symb. Comput. 15(2): 143–167 (1993).
- D. Wang. Computing Triangular Systems and Regular Systems. Journal of Symbolic Computation 30(2) (2000) 221–236.
- Yang, L., Zhang, J. (1994). Searching dependency between algebraic equations: an algorithm applied to automated reasoning. Artificial Intel ligence in Mathematics, pp. 14715, Oxford University Press.